skysunsand
- 38
- 0
Homework Statement
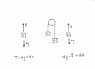
A cord passing over a frictionless, massless pulley has a 4.0 kg object tied to one end and a 12 kg object tied to the other. Compute the tension and acceleration in the cord.
Right now, I'm just trying to calculate the acceleration. It is supposed to be 4.9 m/s^2
Homework Equations
F=ma
T1=T2=0
T1-mg=ma
T2-mg=ma
The Attempt at a Solution
For the 4kg block-
F=ma
T1-mg = ma
T1-39.2 = 4a
Solving in terms of T1 to get
T1= 4a+39.2
For the 12kg block-
F=ma
T2-mg = ma
T2-117.6= 12a
Solving in terms of T2-
T2= 12a+ 117.6
Now, because T1=T2, I can say
12a+ 117.6 = 4a+ 39.2
But then I end up with a=9.8.
The answer is 4.9, which, incidentally, is 9.8/2.
Do I have to divide by 2 because I have two cords? Or is there some other reason I am missing?