Computing the Inverse Laplace Transform

[audifanatic51]

Hi, I recently posted another question about a Laplace transform and now have a question about taking the inverse Laplace transform. Again, my professor did not cover this topic as well as I could have hoped for, and so I am stuck on this problem as well. Again, I understand the idea of Laplace transforms (and their inverses) very well, however actually computing them seems to be another issue. Anyway, here is the problem.

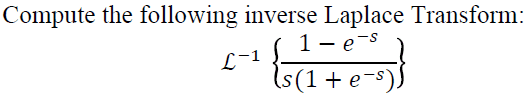
I saw a definition in the book that seemed like it could be useful, however, when I tried to implement it, things seemed to get ugly. Here's the definition I found:

\ell^{-1} \left\{\stackrel{F(s)}{s}\right\} = \int^{t}_{0} f(\tau) d\tau

Please note that due to my typing incompetency, I cannot figure out how to make fractions with the forum tools. That should be F(s)/s in the inverse Laplace transform brackets above.

Any help or step in the right direction would be appreciated. thanks

 

[sunjin09]

Since you have that formula, you observe in your problem that F(s)=(1-exp(-s))/(1+exp(-s)), which can be inverted by a little manipulation (and table look up). Then F(s)/s is inverted by integrating f(tau).