Congruent worldlines in "static" gravitational field

[Shirish]

I'm reading Carroll's GR book and can't quite understand one particular statement. I'll summarize for context:

There's a tower with a physicist at the base and one at the top. Ground guy emits a beam of light with wavelength $\lambda_0$ from height $z_0$, which travels to the top of the tower at height $z_1$. The time between the beginning and end of the emission of any wavelength of light is $\Delta t_0=\lambda_0/c$ (measured w.r.t. a clock at the base). The time interval for the absorption of that wavelength is $\Delta t_1=\lambda_1/c$ (measured w.r.t. a clock at the top). Since we imagine that the gravitational field is static, the paths through spacetime followed by the leading and trailing edge of the single wave must be precisely congruent.

The spacetime diagram is like this:

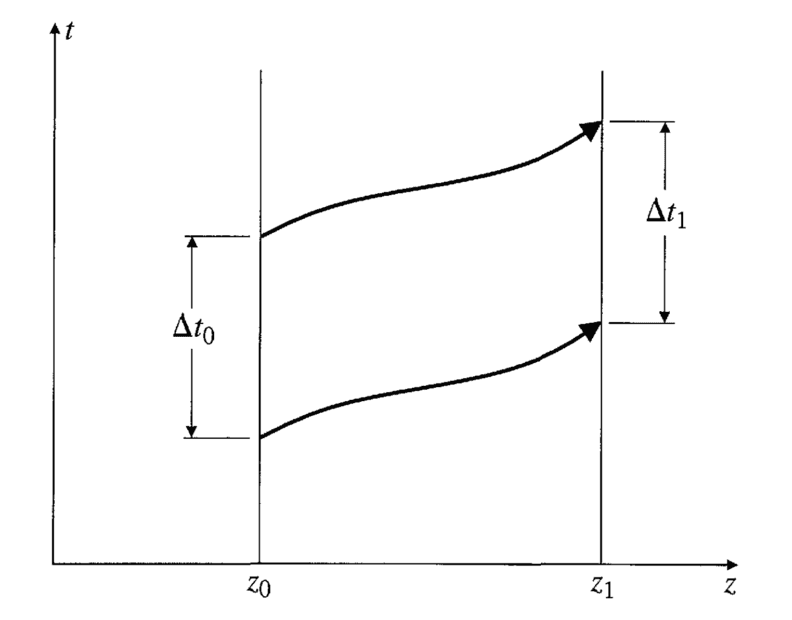
I did not understand the line in bold. Could anyone please explain what's the reasoning behind that statement?

 

[A.T.]

I did not understand the line in bold. Could anyone please explain what's the reasoning behind that statement?

Same spatial path traveled at the same speed profile in the same space-time geometry, just at a different time, means the world-line has the same shape, and is just shifted along the time dimension.

 

[Shirish]

Same spatial path traveled at the same speed profile in the same space-time geometry, just at a different time, means the world-line has the same shape, and is just shifted along the time dimension.

So my takeaway is that: Effectively "static gravitational field" is a misnomer. What was meant is that spacetime looks the same everywhere (i.e. the $t$ and $z$ axes are straight and the coordinate lines are all straight). An uneven gravitational field but with Euclidean spacetime would still give congruent worldlines, but even a uniform gravitational field but in curved spacetime would give non-congruent worldlines.

Is my understanding okay or any corrections?

 

[A.T.]

Effectively "static gravitational field" is a misnomer.

"Static gravitational field" means that it doesn't change over time, so the end of the signal encounters the same space-time-geometry as the begin of the signal, which was sent earlier.

 

[vanhees71]

A gravitational field is called static, if you can find coordinates such that the metric coeffcients don't depend on the time-like coordinate.

 

[Shirish]

"Static gravitational field" means that it doesn't change over time, so the end of the signal encounters the same space-time-geometry as the begin of the signal, which was sent earlier.

Sorry in advance if I sound naive. But at that point in the book, the author is trying to justify why spacetime is curved. Of course after fully reading the book one would know that gravity curves spacetime, so light would get affected by that curvature.

But assuming that we are yet to justify that spacetime is curved, why should we assume that light would care about gravity? With this incomplete knowledge, I can just say that light doesn't care if gravity is static in time or if even there is any gravitational field.

What I'm saying is, I think that the author's argument already assumes that light's path cares about gravity (in turn assuming spacetime curvature), so wouldn't it be a circular argument?

 

[PeterDonis]

at that point in the book, the author is trying to justify why spacetime is curved

The argument he is using actually might not quite show that. See this previous thread discussing a similar argument (originally due to Schild) presented in MTW:

https://www.physicsforums.com/threa...me-dilation-imply-spacetime-curvature.919181/

assuming that we are yet to justify that spacetime is curved, why should we assume that light would care about gravity?

If gravity is spacetime curvature, then everything has to care about gravity, because the spacetime geometry has to be the same whether it's light moving through it or something else. That's not an issue with the argument being presented.

 

[Shirish]

If gravity is spacetime curvature, then everything has to care about gravity, because the spacetime geometry has to be the same whether it's light moving through it or something else. That's not an issue with the argument being presented.

I agree. But what I was trying to say was... Everything caring about gravity is predicated on "gravity is spacetime curvature", and since the author is trying to justify that gravity is spacetime curvature, we can't yet assume whatever follows from it. Which means we can't yet assume that everything has to care about gravity. Hence the confusion...

 

[PeterDonis]

Everything caring about gravity is predicated on "gravity is spacetime curvature"

Not really, although I did state it that way--I should have stated it more generally before. It's actually just based on the equivalence principle. The path of light in an accelerated spaceship in free space would bend, so it must also bend in a room sitting at rest (and with the same proper acceleration) in a gravitational field.

By the time the argument under discussion was first stated (AFAIK that was by Schild in a series of papers in the early 1960s--I give references in the other thread I linked to), there was already plenty of evidence that light obeyed the EP just like everything else, so making that assumption in the argument was not at all controversial. It was actually much more of a leap of faith for Einstein to make it in deriving GR back in the early 1900s.

 

[Ibix]

What was meant is that spacetime looks the same everywhere (i.e. the $t$ and $z$ axes are straight and the coordinate lines are all straight). An uneven gravitational field but with Euclidean spacetime would still give congruent worldlines, but even a uniform gravitational field but in curved spacetime would give non-congruent worldlines.

No. You can always draw straight axes on a map of the nastiest twistiest spacetime you can imagine (as long as you avoid coordinate singularities and the like). The axes won't necessarily be straight in the real world!

The point about these axes is that if you follow the timelike axis or any line parallel to it, you will always "see" the same gravitational foeld around you. So if you hover above an idealised spherical Earth you will find any gravitational experiment you do (throwing a ball, for example) always has the same outcome. Contrast with the real world, where you will feel a varying pull from the Sun and moon and planets, and even density variation in the Earth. The former is a static field, the latter is not.

So the point Carroll is making is that the light paths must be the same because nothing has changed during the experiment. So whatever path the light follows (whether it interacts with gravity or not) must be the same.

You can then, as Peter says, make an argument that we believe that the light path must curve locally because we believe the equivalence principle.

 

[PeterDonis]

What was meant is that spacetime looks the same everywhere

No, that's not what "static" means. It only means that the spacetime geometry is the same along particular curves, in this case the worldlines of observers who are "hovering" at a constant altitude above the gravitating mass. But observers at different altitudes can observe different spacetime geometries--the geometry doesn't change along any particular observer's worldline, but it can change if we switch from one observer to another.

(The technical way of stating the above is that a static spacetime has a timelike Killing vector field, and the worldlines of the observers described above are integral curves of that field.)

 

[Shirish]

So the point Carroll is making is that the light paths must be the same because nothing has changed during the experiment. So whatever path the light follows (whether it interacts with gravity or not) must be the same.

I understood the rest of your post. The above quote is the key though. I think "whether it interacts with gravity or not" is the key distinction. From the naive PoV of someone who doesn't know that a changing gravitational field curves spacetime, if light didn't interact with gravity, then even a changing gravitational field wouldn't affect the light. Peter's answer clarified for me that curved spacetime isn't really a pre-requisite for saying that light interacts with gravity (the equivalence principle is) - which was my misconception.

So the way I now understand Carroll's argument is (again please correct me if I'm wrong) - light interacts with gravity. In the thought experiment we imagine that the gravitational field isn't changing with time (static). So the light wave's leading and trailing edge should behave exactly the same and follow the same path through spacetime => worldlines congruent. But we don't actually observe congruent worldlines => suggesting that the spacetime manifold may not be flat like a typical spacetime diagram suggests, but curved (accordingly the spacetime diagram will have some curved coordinate lines)

 

[Ibix]

In the thought experiment we imagine that the gravitational field isn't changing with time (static).

Yes.

So the light wave's leading and trailing edge should behave exactly the same and follow the same path through spacetime => worldlines congruent.

Yes.

But we don't actually observe congruent worldlines

No. That's the point. Those worldlines are congruent - they must be because nothing changed in the experiment. Gravity didn't change, neither physicist moved, nothing got in the way. If you do the same thing twice under the same circumstances the results must be the same, so the paths must be the same.

But the equivalence principle tells me that the guy at the top must wait longer between the pulses than the guy at the bottom in a locally-SR universe, so I have discovered gravitational time dilation.

 

[PeterDonis]

we don't actually observe congruent worldlines

Actually, the worldlines that aren't congruent are the timelike worldline segments of the lower and upper observers between the two light pulses; as @Ibix notes, the upper observer's worldline segment is longer. That is the part that, at least according to the argument, indicates that spacetime must be curved in the presence of gravitational time dilation (because if spacetime were flat the upper and lower observers' worldline segments would be the same length).

However:

the equivalence principle tells me that the guy at the top must wait longer between the pulses than the guy at the bottom in a locally-SR universe, so I have discovered gravitational time dilation

And what you've also discovered is that the argument as I've just stated it above can't be right, because you've just described a situation in flat spacetime that has the same property--gravitational time dilation--that the argument is using to deduce that spacetime is curved!

The previous thread I linked to earlier was one that I started based on that exact observation. The thread is a long one, but I think the upshot was that you need to add more assumptions to the argument to make it a valid one; just gravitational time dilation by itself isn't enough.

 

[A.T.]

With this incomplete knowledge, I can just say that light doesn't care if gravity is static in time or if even there is any gravitational field.

No, with incomplete knowledge, you cannot just assume that light doesn't care about gravity. You have to include this possibility and thus make sure that gravity is the same for begin and end, so any effects cannot be attributed to a change of the gravitation field.

 

[vanhees71]

Not really, although I did state it that way--I should have stated it more generally before. It's actually just based on the equivalence principle. The path of light in an accelerated spaceship in free space would bend, so it must also bend in a room sitting at rest (and with the same proper acceleration) in a gravitational field.

One should also note that the equivalence principle is a local principle. The upshot of all the discussions about "the equivalence principle" in GR, i.e., more specifically Einstein's equivalence principle is that at any point in spacetime there are the usual inertial frames of reference, where the physics of SR is valid locally, i.e., when considering "sufficiently small" spacetime neighborhoods of this event.

As an accelerated observer you can distinguish a true gravitational field from the mere acceleration of your reference frame against the inertial frames of a Minkowski space by looking at somwhat larger spacetime neighborhoods around you and maybe finding "tidal effects", indicating the presence of a true gravitational field, describing the gravitational interaction of your equipment with some matter around.

 

[A.T.]

And what you've also discovered is that the argument as I've just stated it above can't be right, because you've just described a situation in flat spacetime that has the same property--gravitational time dilation--that the argument is using to deduce that spacetime is curved!

In simple terms:

- Intrinsic space-time curvature is associated with gravitational tidal forces, or non-uniform gravity.
- Gravitational time dilation is associated with gravitational potential differences, or any non-zero gravity.

Uniform gravity (in a local experiment near a mass or for an accelerated frame in empty space), doesn't involve space-time curvature, but since there is a potential difference there is gravitational time dilation. But once you try to to expand the local experiment, so that gravity becomes non-uniform, intrinsic space-time curvature is introduced.

 

[vanhees71]

This brings me to the interesting question, what "uniform gravity" means in GR, i.e., beyond the Newtonian approximation.

 

[Shirish]

Thanks @A.T. , @PeterDonis , @Ibix , @vanhees71 for the responses! Since I'm a newbie to GR, I confess I'm not able to fully follow your replies sometimes (stuff like gravitational time dilation or timelike worldline segments, etc.). I'll continue to study the Carroll book, get a better understanding and then re-read both this thread. I'm sure it will start making sense to me gradually by then.

 

[Nugatory]

This brings me to the interesting question, what "uniform gravity" means in GR, i.e., beyond the Newtonian approximation.

How about: Uniform gravity is what is observed within an idealized Einstein's elevator in flat spacetime?

 

[PeterDonis]

Uniform gravity is what is observed within an idealized Einstein's elevator in flat spacetime?

That's the most common definition I've seen in the literature, but it does have the odd feature that this so-called "uniform" gravity is not actually uniform! The "acceleration due to gravity" varies with height in the elevator.

AFAIK there is no GR solution which has truly uniform gravity, with the "acceleration due to gravity" being the same everywhere.

 

[A.T.]

AFAIK there is no GR solution which has truly uniform gravity, with the "acceleration due to gravity" being the same everywhere.

In Newtonian gravity there is the uniform gravity example inside an off-center spherical cavity, within a spherical mass of uniform density. I wonder if anyone ever tried to solve this in GR, even approximately.

 

[vanhees71]

That sounds awfully complicated, i.e., there seems not to be "enough symmetry" to hope for an exact analytic solution of the EFEs.

 

[PeterDonis]

I wonder if anyone ever tried to solve this in GR, even approximately.

AFAIK no exact solution is known for this case and it would have to be solved numerically (but I'm not aware of any attempt to do so in the literature). My intuitive guess would be that GR corrections would create tidal effects that are not present in the Newtonian case. This is what happens in the GR version of another Newtonian "uniform field" case, the field of an infinite flat plate.

 

[pervect]

I agree. But what I was trying to say was... Everything caring about gravity is predicated on "gravity is spacetime curvature", and since the author is trying to justify that gravity is spacetime curvature, we can't yet assume whatever follows from it. Which means we can't yet assume that everything has to care about gravity. Hence the confusion...

Relativisitc theories of gravitation in which light does not bend certainly do exist, consider for example Nordstrom's theory of gravitation, https://en.wikipedia.org/wiki/Nordström's_theory_of_gravitation.

Of course, in practice, this is a problem, because experimentally we know that light does bend, and a theory in which it doesn't isn't so interesting because it contradicts experiment, even though it's logically possible.

So part of the issue here is whether you are talking about just understanding General Relativity, or whether you mean to understand all possible theories of gravitation. Or perhaps you wish to restrict yourself a bit, and consider only metric theories of gravitation. I would argue that it's better to just think about metric theories, which is how I'll proceed.

The specific version of the wiki I'm quoting is https://en.wikipedia.org/w/index.php?title=Nordström's_theory_of_gravitation&oldid=1110420553

There is another can of worms to perhaps open here, though the worms will probably escape - i.e, I may open the can, but I won't necessarily wrap things up neatly. This is the issue of the relation of the metric to physical observables.

If we relax the idea that the metric must directly give the physical observables of distance, and time, we can for instance fit Nordstrom's theory into a mold of a scalar field on a flat Minkowskii backround.

Another feature of Nordström's theory is that it can be written as the theory of a certain scalar field in Minkowski spacetime

It has been suggested that one might do the same in GR, at least for limited patches of space-time, though it's rather unlikely that one can encapsulate the geometry of a Schwarzschild black hole in this manner. There have been past PF threads about the idea of gravitation as being "Funky fields in Minkowskii space-time", funky because they're not so simple or so well defined as the example in Nordstrom's theory.

Curvature can be and probably should be thought of as arising from the connection, but I find it useful, in my thinking, to consider only the Levi-Civita connection. Given this assumption, one can regard curvature as arising from a single scalar interval arising from the metric. Then I think some of the confusion becomes a bit clearer. If the invariant interval arising from the metric is regarded to be the same as physical measurements of time and distance, then space-time must be curved and can't be flat Minkowskii space-time.

(note that I am taking the position in that the SI scheme of things, c is a units conversion constant, and time and distance are basically the same thing).

If we loosen the relationship between physical observables and the mathematical invariants of the metric, there are more logical possibilities. But whether these additional logical possiblities really turn out to be useful is another matter. I would venture the opinion that so far, they have not been proven useful. And chasing these wriggling worms out of the opened can will probably waste time. But if you've got the time to waste, maybe you might catch something chasing them out of the can. I'd guess not, but who knows.[/quote][/quote]

 

[vanhees71]

Relativisitc theories of gravitation in which light does not bend certainly do exist, consider for example Nordstrom's theory of gravitation, https://en.wikipedia.org/wiki/Nordström's_theory_of_gravitation.

Of course, in practice, this is a problem, because experimentally we know that light does bend, and a theory in which it doesn't isn't so interesting because it contradicts experiment, even though it's logically possible.

Einstein early on abandoned scalar theories of gravitation, because it doesn't admit the realization of the equivalence principle(s).

 

[cianfa72]

No, that's not what "static" means. It only means that the spacetime geometry is the same along particular curves, in this case the worldlines of observers who are "hovering" at a constant altitude above the gravitating mass. But observers at different altitudes can observe different spacetime geometries--the geometry doesn't change along any particular observer's worldline, but it can change if we switch from one observer to another.

Do you mean the local spacetime geometry as seen locally from an observer along a particular path through spacetime ?

 

[PeterDonis]

Do you mean the local spacetime geometry as seen locally from an observer along a particular path through spacetime ?

Yes,

 

[pervect]

So my takeaway is that: Effectively "static gravitational field" is a misnomer. What was meant is that spacetime looks the same everywhere (i.e. the $t$ and $z$ axes are straight and the coordinate lines are all straight). An uneven gravitational field but with Euclidean spacetime would still give congruent worldlines, but even a uniform gravitational field but in curved spacetime would give non-congruent worldlines.

Is my understanding okay or any corrections?

"Static", in the context of "a static space-time", has a well-defined mathematical meaning. Your attempt at a description, in my opinion, does not have a well-defined mathematical meaning. Thus, while it may make sense to you personally , it's hard to say what conclusions you might draw from your definition, and whether or not those conclusions would be correct.

The "irrotational" part of the defintion doesn't seem very relevant to me, unless I'm missing something, by the way. So I'll ignore it.

The current wiki defintion seems reasonably good to me, it would be better to get a better reference for the defintiion of "static space-time"

In general relativity, a spacetime is said to be static if it does not change over time and is also irrotational. It is a special case of a stationary spacetime, which is the geometry of a stationary spacetime that does not change in time but can rotate. Thus, the Kerr solution provides an example of a stationary spacetime that is not static; the non-rotating Schwarzschild solution is an example that is static.

Wiki also offers a definition in terms of coordinates - my take on your thought process is that you "think" in coordinates. I'll use slightly different notation than wiki's. Wiki's general definition is:

$$g(t,\vec{x}) = -\beta(\vec{x})*dt^2 + G(\vec{x})$$

Here $\beta$ is any positive function, G is any positive-definite matrix.

It might be clearer to use a less general definition, where we insist on a specific choice of spatial coordinates that diagonalizes G, namely:

$$g(t, \vec{x}) = -\beta(\vec{x}) + dx^2 + dy^2 + dz^2$$

The first defintion is more general, in that it admit the use of spherical or cylindrical (or any other sort) of coordinates.

The point of the first defintion is that if you choose to use spherical or cylindrical coordinates for the spatial part of your space-time, it doesn't change whether or not the space-time is static. The property of being static (or not static) is a property of the space-time, independent of the coordinates.

But if you're used to coordinate dependent defintions, as your post seems to imply, the second defintion may be easier to grasp.

What the second defintion does is that it imposes a particular choice of coordinates on the postive definite matrix G. Your remarks about "straight lines" leads me to believe that your thinking is along these lines. We might say that it is possible to choose a set of coordinates for the spatial part of the matrix that makes them Cartesian coordinates.

Carrol's statement follows directly from the mathematical definitions - the mapping t-> t + $\Delta$ t gives the congruence relationship between the top and bottom curves. The fact that the spatial part of the metric is exactly the same for both curves means that given two points p1 and p2 which have some distance d in "space" (time = t1) for the bottom curve, when we use the mapping $t -> t +$\Delta## t to transform points to the top curve (at a new time t') the transormed points p1' and p2' have the same distance d between them that they used to have on the bottom curve.

 

[PeterDonis]

Effectively "static gravitational field" is a misnomer. What was meant is that spacetime looks the same everywhere (i.e. the $t$ and $z$ axes are straight and the coordinate lines are all straight).

I picked up on this late, but no, that is not what a static gravitational field means. The gravitational field around an idealized spherical, non-rotating planet or star is static, but it is not the same everywhere--spacetime curvature is larger as you get closer to the planet.

What static does mean is that, as Carroll describes, you can take a path in spacetime between two events, such as the emission and reception of a beam of light between two points fixed in space (where here "fixed" means at rest relative to the source of gravity, the planet or star or whatever), and translate it in time, and the time translated path will have the same shape and length as the original. That is what the text you bolded in your OP is describing.

An uneven gravitational field but with Euclidean spacetime would still give congruent worldlines

There is no such thing as "Euclidean spacetime". If you mean flat spacetime, by definition there is no spacetime curvature in flat spacetime so the issues under discussion cannot even arise.

even a uniform gravitational field but in curved spacetime would give non-congruent worldlines.

There is no such thing as "a uniform gravitational field in curved spacetime".

 

[cianfa72]

No. You can always draw straight axes on a map of the nastiest twistiest spacetime you can imagine (as long as you avoid coordinate singularities and the like). The axes won't necessarily be straight in the real world!

I would like to point out that when you see a map on a piece of paper you have to know how that map is actually built (i.e. what map it is). In the case of post#1 it is the inertial/Minkowski map for Minkowski/flat spacetime.

 

[Ibix]

would like to point out that when you see a map on a piece of paper you have to know how that map is actually built (i.e. what map it is).

Indeed.

In the case of post#1 it is the inertial/Minkowski map for Minkowski/flat spacetime.

No, it's in an arbitrary static spacetime in coordinates that reflect that symmetry. In context, it's probably Schwarzschild spacetime in Schwarzschild coordinates, but the argument is more general.

 

[cianfa72]

No, it's in an arbitrary static spacetime in coordinates that reflect that symmetry. In context, it's probably Schwarzschild spacetime in Schwarzschild coordinates, but the argument is more general.

Why ? If you assume Schwarzschild spacetime in Schwarzschild coordinates then spacetime is curved and that's actually what that argument is supposed to show (i.e. give a proof).

 

[Ibix]

If you assume Schwarzschild spacetime in Schwarzschild coordinates then spacetime is curved and that's actually what that argument is supposed to show (i.e. give a proof).

I was stating the eventual conclusion there. The only assumption being made is that observers at any fixed $z$ always see the same result of any gravitational experiment (so the lines of constant $z$ are what we will eventually call integral curves of the timelike Killing vector field). That's why the light paths are the same. But we aren't assuming anything about what those paths are, which is why they are drawn as arbitrary squiggles.

If the experiment is being carried out in vacuum over a spherical body this will inevitably turn out to be Schwarzschild spacetime. But we aren't assuming that at this stage.

 

[cianfa72]

The only assumption being made is that observers at any fixed $z$ always see the same result of any gravitational experiment (so the lines of constant $z$ are what we will eventually call integral curves of the timelike Killing vector field). That's why the light paths are the same.

Ok, so the lines of constant $z$ in the map represent (in the map) the integral curves of the timelike KVF -- a 'static' spacetime also requires that the timelike KVF is hypersurface orthogonal. Basically the values of $z$ "label/ identify" each of those timelike KVF's integral curves.

The point I do not catch is that the obsever at fixed $z$ doesn't see the path of the light coming from the bottom ($z=0$)...