- #1
kevindin
- 10
- 0
I'm looking for an expression for the deflection of light in a static gravitational field.
Referring to 'deflection of star light past the sun' in Sean Carroll's "Spacetime and Geometry" - equation 7.80 for the "transverse gradient":
[itex]
\nabla\perp\phi = \frac{GM}{(b^2 + x^2)^{3/2}}\vec b
[/itex]
Deflection angle is
[itex]
\alpha = {2GMb} \int {\frac{dx}{(b^2 + x^2)^{3/2}}}
= \frac{4GM}{b}
[/itex]
As far as I understand it, this is only valid for weak fields/small deflection. I'd like to plot photon paths in strong fields (with just a single point mass, not distributed), so I'm looking for the instantaneous deflection, which I'll plot/integrate numerically, based on mass, radial distance from mass, and angle of photon trajectory. It should not use the Schwarzschild metric, because I don't want the singularity at r=Rs and it only needs to be in 2 dimensions, because of spherical symmetry. So, is there an expression for the polar coordinates r2, θ2 and trajectory a2, for a photon traveling from p1 to p2, using M, r1, θ1, a1, L?
I've attached a diagram which I hope illustrates it:
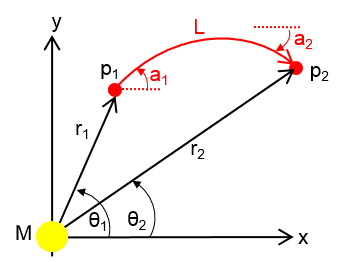
Many thanks
Kevin
Referring to 'deflection of star light past the sun' in Sean Carroll's "Spacetime and Geometry" - equation 7.80 for the "transverse gradient":
[itex]
\nabla\perp\phi = \frac{GM}{(b^2 + x^2)^{3/2}}\vec b
[/itex]
Deflection angle is
[itex]
\alpha = {2GMb} \int {\frac{dx}{(b^2 + x^2)^{3/2}}}
= \frac{4GM}{b}
[/itex]
As far as I understand it, this is only valid for weak fields/small deflection. I'd like to plot photon paths in strong fields (with just a single point mass, not distributed), so I'm looking for the instantaneous deflection, which I'll plot/integrate numerically, based on mass, radial distance from mass, and angle of photon trajectory. It should not use the Schwarzschild metric, because I don't want the singularity at r=Rs and it only needs to be in 2 dimensions, because of spherical symmetry. So, is there an expression for the polar coordinates r2, θ2 and trajectory a2, for a photon traveling from p1 to p2, using M, r1, θ1, a1, L?
I've attached a diagram which I hope illustrates it:
Many thanks
Kevin
Last edited: