Conservation Linear Momentum (? Book Error ?)

[Stobbe]

Ok, don't ask why I was doing this dynamics problem from an old textbook, but, I cannot get the answer to match that in the back of book and it's a simple problem.

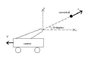
Here it is, a cannon weighing 400 lb, fired a cannon ball weighing 10 lb, and had a muzzle velocity of 200 ft/s. For a 10 degree elevation angle, determine the velocity of the cannon after it was fired?

My immediate though was conservation of linear momentum, with Mc*Vcx + Mb+Vbx = 0, where the subscript c, b, and x are cannon, cannon ball, and horizontal direction, respectively.

Substituting the following values
Mc = 400lb
Mb = 10lb
Vbx = 200*sin(10^o)

and solving for Vcx
yields -4.9240 ft/s (sign is relative to coordinate system)

however the back of the book is stating -4.80 ft/s, WTF am I doing wrong?

 

[mukundpa]

I think, the elevation of the barrel is 10 degree but the shot is not leaving the barrel at 10 deg. with the horizontal because of recoiling of the gun. The angle of projection is more than 10 degree with horizontal and hence Vbx = 200*sin(10^o) is not correct.

 

[mukundpa]

moreover the horizontal component is not sin@ but cos@.

Muzzle speed is relative to the berral

The book is giving correct answer.

 

[zzzzzz]

moreover the horizontal component is not sin@ but cos@.

And with this, you find the same result given by your book

v=20 ft/s
M= cannon mass
m= cannonball mass
V= cannon speed

Conservation of momentum in the x direction requires (absolute values):

mxv=MxV

which leads to:

V=[cos(10°)x200ft/sx10lb]/400lb=4.924 ft/s


Now… what about the vertical (i.e. y) v-component? The mxvxsin(10°) momentum seems to have no "counterpart"

 

[mukundpa]

Sorry ZZZZZ

During the process of firing, the cannon starts recoiling and acquirs a velocity v_c and hence the velocity of ball relative to Earth in horizontal direction after leaving the cannon will be v_b\cos \theta - v_c

The vertical component of velocity will remains the same that is why the angle of projection will be greater then the angle of elevation of the barrel, as I gave in previous posting.

Now conserving the linear momentum

m(v_b\ cos\theta - v_c)\ = M v_c

gives
v_c = \frac{m v_b cos\theta}{M + m}
= 4.8 f/s negative is due to direction, arrange.

It is a well known problem asking about the direction of the ball leaving the gun.

 

[zzzzzz]

Ahaaa, got it... I read the first post too quickly and I thought that 4.9240 ft/s was the answer in the book... actually zzzzzz means that I'm most of the time asleep and I should wake up before reading. Excuse me

 

[Stobbe]

Got It

Thanks mukundpa and zzzzz,

The sin cos thing was a typo but the velocity difference is essential to conserving the location of the center of mass of the system (ie. conservation linear momentum). I can't believe I missed that,

Thanks