Conservation of angular and linear momentum

[wudingbin]

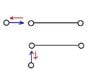
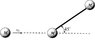
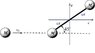
a rigid massless rod of length L joins two particles each of mass M. The rod lies on
a frictionless table, and is struck by a particle of mass M and velocity v0. After the collision, the projectile moves straight back. Find the
angular velocity of the rod about its center of mass after the collision, assuming that
mechanical energy is conserved.

i tried to solve this question using the conservation of linear momentum first.
using ((m-2m)/3m)v0 to find the speed of the mass M after collision.
(2m/3m)v0, to find the speed of the rod after collision.
translational speed of the rod = (2/3v0 - wr)
angular speed of the rod = w

hence i used the conservation of energy method to solve for w.
however, my answer is incorrect. may i know which part, i am wrong

 

[ehild]

You got the velocity of the particle after collision correctly: it is -Vo/3.
The velocity of the rod is also correct, but it is the velocity of the CM : Vcm=2/3 Vo.
I do not understand what you mean on "translational speed of the rod". You need to use conservation of angular momentum.

ehild

 

[wudingbin]

You got the velocity of the particle after collision correctly: it is -Vo/3.
The velocity of the rod is also correct, but it is the velocity of the CM : Vcm=2/3 Vo.
I do not understand what you mean on "translational speed of the rod". You need to use conservation of angular momentum.

ehild

hi sir, if Vcm= 2/3Vo. then according to the conservation of mechanical energy, rotation of the rod could nt happen.
the translation speed is Vcm.

 

[tiny-tim]

You got the velocity of the particle after collision correctly: it is -Vo/3.
The velocity of the rod is also correct, but it is the velocity of the CM : Vcm=2/3 Vo.

isn't it the other way round? …

the rod is heavier, so it'll move less ​

 

[ehild]

hi sir, if Vcm= 2/3Vo. then according to the conservation of mechanical energy, rotation of the rod could nt happen.
the translation speed is Vcm.

Sorry, I misunderstood the problem. Your results are correct if the projectile hits the rod at its end, parallel to it, like in the first picture. Then the angular momentum really stays zero. Is not said anything where the incoming particle hits the rod and about the direction of Vo with respect to the rod? Was not it meant as in the second picture?

ehild

 

[wudingbin]

sorry sir, i should have upload the diagram earlier. the projectile hit the rod at 45 degree

 

[ehild]

That is a difference! Set up a coordinate system, as in the picture for example. The linear momentum of he incoming particle has only x component before and after the collision, and it has some angular momentum with respect to the origin. The angular momentum is also conserved in the collision. Write up the equation for the angular momentum of the whole system in addition to the equations for linear momentum and KE. ehild

 

[wudingbin]

hi sir,
i think i made a big conceptual mistake, thinking that the linear collision is elastic which is not, because some of the inital linear kinetic energy is converted into rotational energy, therefore the final linear speed of the projectile should not be calculated using elastic collision formula. i gt my answer now, thank a lot for the help.

 

[ehild]

I am pleased that you solved the problem. Conservation of energy is valid, but the rotational energy has to be included.
For the sake of other people reading this thread could you please show your solution ?

ehild