iamkristing
- 33
- 0
[SOLVED] conservation of energy
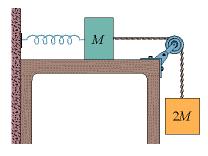
Two blocks, of masses M = 1.9 kg and 2M are connected to a spring of spring constant k = 220 N/m that has one end fixed, as shown in the figure below. The horizontal surface and the pulley are frictionless, and the pulley has negligible mass. The blocks are released from rest with the spring relaxed.
(a) What is the combined kinetic energy of the two blocks when the hanging block has fallen a distance of 0.090 m?
J
(b) What is the kinetic energy of the hanging block when it has fallen that 0.090 m?
J
(c) What maximum distance does the hanging block fall before momentarily stopping?
m
k=(1/2)mv^2
u=mgh
ki + ui = kf + uf
I solved A using u(grav) =kf +us and got 2.7 J
For B i got 1.8 J
C is where I have a problem. I know the kinetic energy must equal zero and somehow you find the height from u=mgh. I just can't seem to connect the two...
Homework Statement
Two blocks, of masses M = 1.9 kg and 2M are connected to a spring of spring constant k = 220 N/m that has one end fixed, as shown in the figure below. The horizontal surface and the pulley are frictionless, and the pulley has negligible mass. The blocks are released from rest with the spring relaxed.
(a) What is the combined kinetic energy of the two blocks when the hanging block has fallen a distance of 0.090 m?
J
(b) What is the kinetic energy of the hanging block when it has fallen that 0.090 m?
J
(c) What maximum distance does the hanging block fall before momentarily stopping?
m
Homework Equations
k=(1/2)mv^2
u=mgh
ki + ui = kf + uf
The Attempt at a Solution
I solved A using u(grav) =kf +us and got 2.7 J
For B i got 1.8 J
C is where I have a problem. I know the kinetic energy must equal zero and somehow you find the height from u=mgh. I just can't seem to connect the two...
Last edited by a moderator: