Conservation of Mechanical Energy

[Travis Enigma]

Homework Statement

A 5.0 g marble is fired vertically upward using a spring gun. The spring must be compressed 8.0 cm if the marble is to just reach a target 20 m above the marble’s position on the compressed spring. (a) What is the change ΔUg in the gravitational potential energy of the marble–Earth system during the 20 m ascent? (b) What is the change ΔUs in the elastic potential energy of the spring during its launch of the marble? (c) What is the spring constant of the spring?

Relevant Equations

Ug= mgh

Okay For a this is what I did.

a.

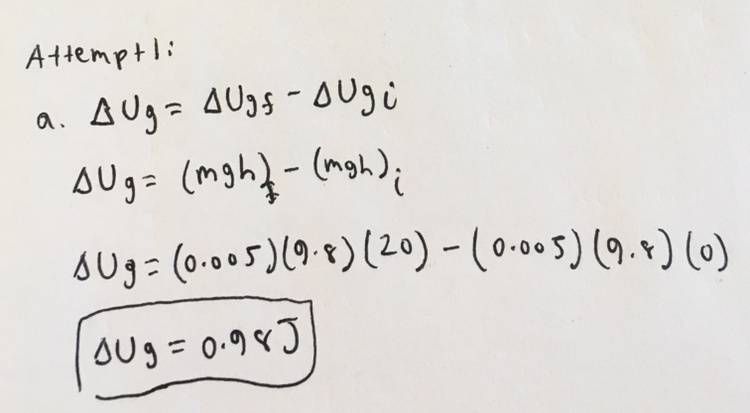
I'm confused about B. I understand that it has something to do with the Conservation of Mechanical Energy, but I don't exactly know what to do.

 

[Travis Enigma]

What exactly is the relationship between gravitational potential energy and elastic potential energy?

 

[Lnewqban]

While compressing the spring of the gun, your muscles are doing certain amount of work that remains stored in the deformed spring.
That "potential" energy is eventually released and fully transferred to the marble.
The same amount of energy is used to elevate the marble certain height, while doing work against gravity.