keroberous
- 15
- 1
Homework Statement
A bomb initially at rest is exploded into three pieces on a smooth, horizontal surface. Two pieces fly off at a 60° angle to each other, a 2.0 kg piece at 20 m/s and a 3.0 kg piece at 12 m/s. The third piece flies off at 30 m/s with an unknown direction. Determine the direction and mass of the third piece.
Homework Equations
conservation of linear momentum
##m_1v_{1x}+m_2v_{2x}+m_3v_{3x}=m_1v'_{1x}+m_2v'_{2x}+m_3v'_{3x}##
and
##m_1v_{1y}+m_2v_{2y}+m_3v_{3y}=m_1v'_{1y}+m_2v'_{2y}+m_3v'_{3y}##
3. The Attempt at a Solution
I have a full solution, but the question doesn't give an answer so I'm not sure if I'm correct.
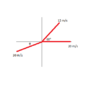
I have attached a picture of how I set up the axes for reference.
Since the bomb was initially at rest my equations become:
##0=m_1v'_{1x}+m_2v'_{2x}+m_3v'_{3x}\\0=(2.0)(20)+(3.0)(12\cos(60))+m_3(-30)\cos\theta\\0=58-30m_3\cos\theta\\m_3=\frac {58} {30\cos\theta}##
and
##0=m_1v'_{1y}+m_2v'_{2y}+m_3v'_{3y}\\0=(2.0)(0)+(3.0)(12\sin(60))+m_3(-30)\sin\theta\\0=31.177-30m_3\sin\theta\\m_3=\frac {31.177} {30\sin\theta}##
Now equating and solving for theta:
##\frac {58} {30\cos\theta}=\frac {31.177} {30\sin\theta}\\\tan\theta=\frac{31.177}{58}\\\theta=28##
And finally, solving for the mass:
##m_3=\frac {58} {30\cos\theta}\\m_3=\frac {58} {30\cos(28)}\\m_3=2.2##
I'd appreciate it if you could give insight into my line of reasoning and final solutions. Thanks!