bXD01Q99
- 2
- 0
Hi, I wanted to make an equation with Newtonian physics, but failed. Here's the problem:
I've done this so far:
Symptoms: the object starts moving with high acceleration, velocity gain speed gets slower over time, and the velocity converges to (and reaches?) its maximum speed. Then, all the additional performace goes, through friction, into heat energy.
The engine gives P \times \Delta t joules of energy every \Delta t time, and friction takes away F_f \times \Delta s. Energy at a given time can be written as:
E = P t - F_f s
\frac{m v^2}{2} = P t - \mu m g s
\frac{m v^2}{2} = P t - \mu m g v_{avg} t ?
s is dependant on t and v, but v depends on the E, which depends on s, so I don't know how to continue. I need to get s and its derivative, v, for any given t time.
So I've tried a temporaty iterational method:
Start with E = 0, v = 0, then, iterate with very small \Delta t time intervals, and do this:
1. to E, add ( P - \mu m g v ) \times \Delta t
2. set v to \sqrt{ 2 E / m }
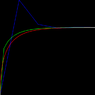
With this algorithm, I've drawn this velocity-time graph:
img182.imageshack.us/my.php?image=47155991qs7.png or [ATTACHMENT]
Iteration count: Blue=5, Green=25, Red=625.
It looks like some sort of logarithmic or root curve.
Well, that's it. If anyone can give me equation instead of an iterating algorithm, and/or also consider slope, drag, and 2D plane vector directions, I'll really appreciate it. Thanks in advance.
Code:
Consider an object with that
^ has [B]m[/B] mass, and a built in
drag & | magic motor that has [B]P[/B]
friction | magic force constant performance. The
<----------[OBJ]-------------> motor is magically propelling
==============|================= the object in a direction,
| gravity parallel with the ground,
v which has [B]u[/B] friction.
Gravity is [B]g[/b].
What is the velocity and the traveled distance after [B]t[/B] time?I've done this so far:
Symptoms: the object starts moving with high acceleration, velocity gain speed gets slower over time, and the velocity converges to (and reaches?) its maximum speed. Then, all the additional performace goes, through friction, into heat energy.
The engine gives P \times \Delta t joules of energy every \Delta t time, and friction takes away F_f \times \Delta s. Energy at a given time can be written as:
E = P t - F_f s
\frac{m v^2}{2} = P t - \mu m g s
\frac{m v^2}{2} = P t - \mu m g v_{avg} t ?
s is dependant on t and v, but v depends on the E, which depends on s, so I don't know how to continue. I need to get s and its derivative, v, for any given t time.
So I've tried a temporaty iterational method:
Start with E = 0, v = 0, then, iterate with very small \Delta t time intervals, and do this:
1. to E, add ( P - \mu m g v ) \times \Delta t
2. set v to \sqrt{ 2 E / m }
With this algorithm, I've drawn this velocity-time graph:
img182.imageshack.us/my.php?image=47155991qs7.png or [ATTACHMENT]
Iteration count: Blue=5, Green=25, Red=625.
It looks like some sort of logarithmic or root curve.
Well, that's it. If anyone can give me equation instead of an iterating algorithm, and/or also consider slope, drag, and 2D plane vector directions, I'll really appreciate it. Thanks in advance.
Attachments
Last edited: