Constraint Relations: Acclerations of Blocks in System

ritwik06
Messages
577
Reaction score
0
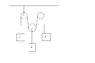
The system is given in the picture. I want to know the relation between the acclerations of each block.

My attempt:
suppose if the body in the middle moves up by x. the string will get loose by 2x. therefore, if a1, a2, a3 are the acclerations. -2*a2=a1+a3
am i correct?
 

Attachments

  • FBD.JPG
    FBD.JPG
    6.2 KB · Views: 435
Physics news on Phys.org
Sounds right to me.
 
But the thing is that my calculated accelerations of the three blocks differ from the answer in my book. Can you please just tell me the acclerations of each block? (in order that I may know if I am right)
 
Show what you did and I'll check it out.
 
Thanks for the help. I actaully was solving with the wrong sign.
 
Thread 'Need help understanding this figure on energy levels'

Thread 'Need help understanding this figure on energy levels'

This figure is from "Introduction to Quantum Mechanics" by Griffiths (3rd edition). It is available to download. It is from page 142. I am hoping the usual people on this site will give me a hand understanding what is going on in the figure. After the equation (4.50) it says "It is customary to introduce the principal quantum number, ##n##, which simply orders the allowed energies, starting with 1 for the ground state. (see the figure)" I still don't understand the figure :( Here is...
View full post »
Thread 'Understanding how to "tack on" the time wiggle factor'

Thread 'Understanding how to "tack on" the time wiggle factor'

The last problem I posted on QM made it into advanced homework help, that is why I am putting it here. I am sorry for any hassle imposed on the moderators by myself. Part (a) is quite easy. We get $$\sigma_1 = 2\lambda, \mathbf{v}_1 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \sigma_2 = \lambda, \mathbf{v}_2 = \begin{pmatrix} 1/\sqrt{2} \\ 1/\sqrt{2} \\ 0 \end{pmatrix} \sigma_3 = -\lambda, \mathbf{v}_3 = \begin{pmatrix} 1/\sqrt{2} \\ -1/\sqrt{2} \\ 0 \end{pmatrix} $$ There are two ways...
View full post »

Similar threads

Constraint relation in a pulley spring system
Replies
6
Views
5K
Pulley system, calculate acceleration
Replies
16
Views
5K
What is the acceleration of the blocks in a pulley constraint problem?
Replies
21
Views
5K
Using Effective Mass to find the accelerations of 3 masses connected by pulleys
Replies
25
Views
3K
Quantum mechanics(expected probability)
Replies
1
Views
2K
A Pair of interacting systems, driven coupled harmonic oscillators
Replies
7
Views
2K
I How Does Parametrization Help Describe Particle Motion in Mathematics?
Replies
3
Views
2K
B I got confused about SR after trying to reply to another
Replies
4
Views
1K
Three weights and two pulley system
Replies
6
Views
3K
Block and Pulley System: Acceleration and Tension Homework Solution
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top