youxcrushxme
- 22
- 0
I'm really confused about this problem -
As shown in Figure 5-22, a force of magnitude 7.50 N pushes three boxes with masses m1 = 1.30 kg, m2 = 3.30 kg, and m3 = 5.10 kg.
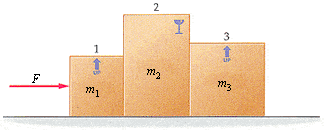
(a) Find the magnitude of the contact force between boxes 1 and 2.
(b) Find the magnitude of the contact force between boxes 2 and 3.
So F=7.5N. First you need to find the acceleration right? So I got a=F/m and did 7.5/(1.3+3.3) for part a. That gave me 1.63. I multiplied that with 3.3 because that's the mass of the second box and got a contact force of 5.379N but it's telling me that it's not right. If anyone could help I'd really appreciate it
As shown in Figure 5-22, a force of magnitude 7.50 N pushes three boxes with masses m1 = 1.30 kg, m2 = 3.30 kg, and m3 = 5.10 kg.
(a) Find the magnitude of the contact force between boxes 1 and 2.
(b) Find the magnitude of the contact force between boxes 2 and 3.
So F=7.5N. First you need to find the acceleration right? So I got a=F/m and did 7.5/(1.3+3.3) for part a. That gave me 1.63. I multiplied that with 3.3 because that's the mass of the second box and got a contact force of 5.379N but it's telling me that it's not right. If anyone could help I'd really appreciate it