Control System Doubt: Voltage Transfer Function of Resistor

[cnh1995]

Consider the following circuit with Vs=1V,
R=1Ω and C=1F.

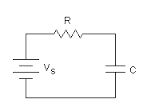
The voltage transfer function of the resistor can be written as
V_r(s)/V_s(s)=s/(s+1).
Now I understand s is complex frequency and at s=∞
the transfer function becomes unity since capacitor acts as a short and V_s=V_r. What I don't understand is at s=-1, the TF becomes infinity.
If s=-1 and s=σ+jω, σ=-1 gives TF=∞. What is the meaning of this? What is the general significance of σ? I know jω represents the oscillations in the system but what does the real part σ represent?

 

[BvU]

Hi,

Usually the Laplace transform is unilateral.

 

[AlexCaledin]

σ is for an exponential voltage (or current) proportional to exp(σt).
Consider the current I=exp(-t).
It gives voltages exp(-t) and -exp(-t)+const passing through the resistor and capacitor - so the sum is constant (1 in your case) which means infinite "AC" gain of your circuit.

(but of course it's only in mathematics where a current can be infinite in the past))