- #1
Abdul Wali
- 33
- 0
HI,
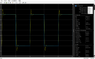
i have a first order controller (ts/ks+k) which contain some oscillations and its settling time is very huge, i wanted the controller to have settling time of 10seconds and remove the oscillations. in order to remove the noise and get the expected settling time i added a filter ( s/cs+1) where c=1/fc where fc=cutoff frequency to the transfer function. during troubleshooting after choosing different values for fc finally i chose fc=100 and it gave me settling time of 10seconds. Now i am not sure and i want to know that how to prove this mathematically ?? or how it happened??Or is it possible to prove it from bodeplot as attached to the link below?
https://drive.google.com/open?id=0B9NQhKDld_D4TjNPNzNoM2I3U28
Your help is appreciated. Thanks in advance.
i have a first order controller (ts/ks+k) which contain some oscillations and its settling time is very huge, i wanted the controller to have settling time of 10seconds and remove the oscillations. in order to remove the noise and get the expected settling time i added a filter ( s/cs+1) where c=1/fc where fc=cutoff frequency to the transfer function. during troubleshooting after choosing different values for fc finally i chose fc=100 and it gave me settling time of 10seconds. Now i am not sure and i want to know that how to prove this mathematically ?? or how it happened??Or is it possible to prove it from bodeplot as attached to the link below?
https://drive.google.com/open?id=0B9NQhKDld_D4TjNPNzNoM2I3U28
Your help is appreciated. Thanks in advance.
Last edited: