Converting Coordinate Systems: Exploring the Force on a Semicircular Conductor

[pobro44]

1. The problem statement, all variables and given/known dana

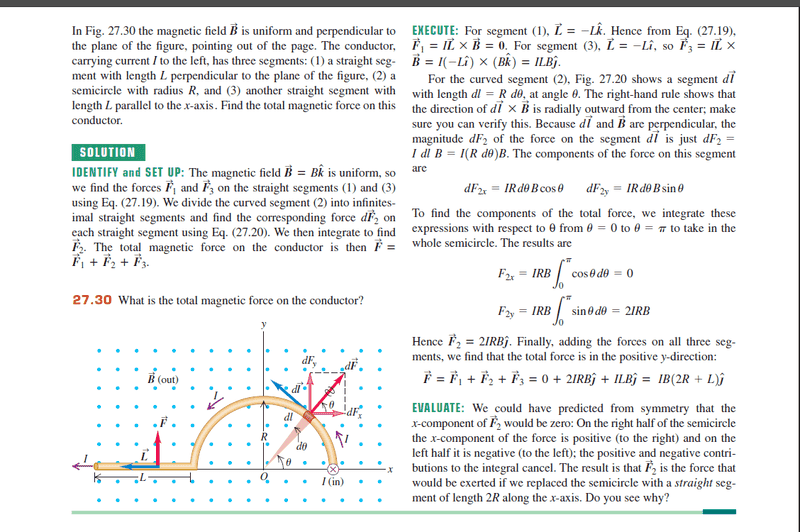
I was revisiting University physics textbook and came across this problem. We learned new coordinate systems in classical mechanics classes so I wanted to see if I can apply this to the problem of force on semicircular part of the conductor

Homework Equations

Cartesian and cylindrical coordinates

The Attempt at a Solution

I tried using cylindrical coordinates. I rewrote radial vector (here marked by s unit vector…in a hurry I dropped the unit vector on second line) in cartesian coordinates and integrated. Result is correct.

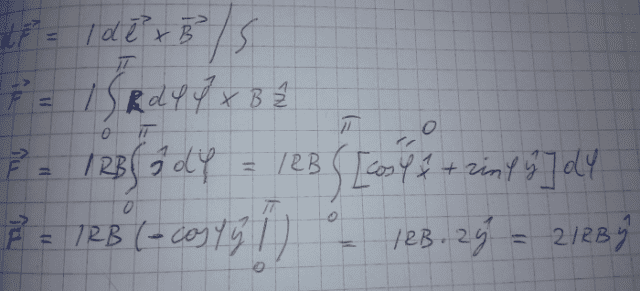
However if I choose not to use conversion to cartesian coordinates and just integrate like this, putting the radial vector in front of integral (now marked with r unit vector) I get the following:

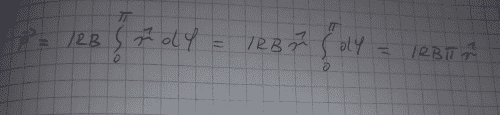So, I have a force in radial direction. Makes sense, it is always directed perpendicular to the semircircle tangent. And it is obvious by symetry that x cartesian components cancel out leaving only y component. However, these 2 results should be the same. If they are, then we should be able to rewrite the cylindrical radial unit vector as 2/pi * y hat unit vector in cartesian coordinates. I may be missing something obvious or made an embarassing mistake, but I see no way to convert the result that way (eliminating pi in particular).

 

[Nathanael]

However if I choose not to use conversion to cartesian coordinates and just integrate like this, putting the radial vector in front of integral (now marked with r unit vector) I get the following:

View attachment 227450

It’s a bit hard to read others’ handwriting. Is that an $\hat r$ that you just took out of the integral? $\hat r$ varies over the integral, so that is an improper thing to do. As you said, by symmetry, only the y component survives. So then integrate just that component.

So, I have a force in radial direction. Makes sense,

How does that make sense when that should be the net force and there are infinite unique “radial direction”s?

 

[Orodruin]

How does that make sense when that should be the net force and there are infinite unique “radial direction”s?

This is a point that cannot be underlined enough times. Without reference to a particular point, talking about a ”radial” direction is meaningless. Would that be the radial direction at the beginning of the half-circle or at the end (those are opposite) or maybe in the middle? It just does not have a well defined meaning to talk about the radial direction for a vector valued integral.

 

[Phylosopher]

I think you chose a bad problem to practice cylindrical coordinates with.

See, the solution at the end depends only on $\hat{j}$, this means if you worked your problem with cylindrical coordinates, at the end you will have more than one basis, which would look awful and without meaning. You will eventually write it back with Cartesian coordinates to have it written with one basis.

I actually understand why you chose cylindrical coordinates. Because we have half a circle, but the symmetry force you back to Cartesian coordinates. Funny right! (of course you can still write it in cylindrical coordinates, but it won't look elegant)

This is a point that cannot be underlined enough times. Without reference to a particular point, talking about a ”radial” direction is meaningless. Would that be the radial direction at the beginning of the half-circle or at the end (those are opposite) or maybe in the middle? It just does not have a well defined meaning to talk about the radial direction for a vector valued integral.

I think, if we are working with vectors inside an integral, the safest thing to do is to transform back to Cartesian coordinates. Since you are sure the bases are independent.

 

[Orodruin]

I think, if we are working with vectors inside an integral, the safest thing to do is to transform back to Cartesian coordinates. Since you are sure the bases are independent.

It is not about bases being independent, it is about the basis being constant. You could perfectly well choose an arbitrary point and express the result in the cylinder basis of that point, but that is just choosing a different fixed basis. In flat spaces, it is posible to do this without ever referencing a Cartesian coordinate system, but that seems rather tedious and unnecessary. Once you go on to curved spaces, integrals like this typically do not make sense at all.

 

[pobro44]

Thank you for all your answers. I believe I get it. I can't take radial unit vector outside the integral, cause it changes around path of integration, and it is obvious that it depends on the angle once I convert it to cartesian coordinates. Only cartesian unit vectors are safe to put in front of integral. Also, while the force is radial on every point of integration path, net force being radial is meaningless, just as although infitesimal part of area vector of a sphere is radial it would make little sense for area of whole sphere to be.