jiten827
- 7
- 0
[SOLVED] Corner Reflector
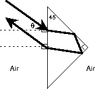
A corner reflector is to be made from a triangular prism with index of refraction n = 1.86, as shown in the diagram below. What is the maximum angle, with respect to the normal to the front surface of the prism, θ, such that total reflection will occur?
n_{air}sin\theta_1 = n_{prism}sin\theta_2
I tried doing
1 * sin\theta_1 = 1.86 * sin\ 90
solving for \theta_1 gives arcsin (1.86) which is undefined.
Any help appreciated
Here is the graphic for the problem
Homework Statement
A corner reflector is to be made from a triangular prism with index of refraction n = 1.86, as shown in the diagram below. What is the maximum angle, with respect to the normal to the front surface of the prism, θ, such that total reflection will occur?
Homework Equations
n_{air}sin\theta_1 = n_{prism}sin\theta_2
The Attempt at a Solution
I tried doing
1 * sin\theta_1 = 1.86 * sin\ 90
solving for \theta_1 gives arcsin (1.86) which is undefined.
Any help appreciated
Here is the graphic for the problem
Attachments
Last edited: