Correct/accurate vector diagram.

[binbagsss]

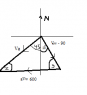
An aeroplane (A) can fly at 600kmh^-1 in still air. It has to fly to an airport which is SW of its current position. There is a wind of 90kmh^-1 blowing from N20W.

a) Find the direction that the plane should take relative to the wind
b) what is the ground speed of aeroplane.

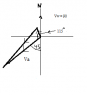
I have attached two diagrams. The difference only being the bearing on which I draw the velocity of the wind.

Diagram 2, where I take the the negative of VW- changing the bearing to S20W is the correct one. What is the exact reason for this?

I have also noticed that whichever diagram I use, lead me to calculate angle x as the same in either case, so the answer to part a in this question, (sin x = sin (130-x) - sin 65 = sin 115)

however that the way in which I chose to draw the diagram determines angle y - via the sine rule determining also the ground speed of the aeroplane.

Help as to why diagram 2 is the correct way is greatly appreciated.

One more thing that I do not quite understand is the direction of aVw in diagram 2. On the diagram to me this looks like : - (-Va) + Vw = Va+ Vw, but I always thought that the direction of this must be in line with Va - Vw.

(as this was drawn through reversing Va initially)

Thanks for any assistance much appreciated !

(Apologies on the diagrams, units to all velocities are kmh^-1 , Va - velocity of aeroplane , VW - velocity of wind.)

 

[LCKurtz]

I would solve the problem using your diagram 1. It will give you the ground speed and the heading of the airplane. From that you can figure out the "direction relative to the wind" of the airplane, which is a strange thing to want if I understand the problem correctly.

 

[binbagsss]

I would solve the problem using your diagram 1. It will give you the ground speed and the heading of the airplane. From that you can figure out the "direction relative to the wind" of the airplane, which is a strange thing to want if I understand the problem correctly.

"direction relative to wind" / "course taken" by the plane, which I thought must be the direction relative to the wind as the direction of VA must be SW. I thought that the question was asking for the path the plane takes relative to the wind to get where he wants whilst compensating for the wind.

In both diagrams 1 and 2 I obtain angle x = [sin 65/600 * 90] = [sin 115/600 * 90] (which is the correct answer) for me to find the dersired bearing,

however with I obtain Va = sin y * 600 / sin 65, but due to the variation in y caused by my diagrams this leads to the 2 different answers - y = 107.2 and y = 57.19 .

Thanks alot.

 

[LCKurtz]

"direction relative to wind" / "course taken" by the plane, which I thought must be the direction relative to the wind as the direction of VA must be SW. I thought that the question was asking for the path the plane takes relative to the wind to get where he wants whilst compensating for the wind.

In both diagrams 1 and 2 I obtain angle x = [sin 65/600 * 90] = [sin 115/600 * 90] (which is the correct answer) for me to find the dersired bearing,

however with I obtain Va = sin y * 600 / sin 65, but due to the variation in y caused by my diagrams this leads to the 2 different answers - y = 107.2 and y = 57.19 .

Thanks alot.

I haven't figured out why your diagram 2 would be relevant.

Perhaps the author does want the bearing the plane flies, which is what you would normally require in a problem such as this. I haven't checked your calculations. For comparison, I get the planes bearing to be 217.18 degrees, measured as a polar coordinate angle and a ground speed of 632.46. He has a bit of a tailwind.

 

[binbagsss]

I haven't figured out why your diagram 2 would be relevant.

Perhaps the author does want the bearing the plane flies, which is what you would normally require in a problem such as this. I haven't checked your calculations. For comparison, I get the planes bearing to be 217.18 degrees, measured as a polar coordinate angle and a ground speed of 632.46. He has a bit of a tailwind.

The bearing is 243.8 degrees, S(52.8)W, the ground speed is 632.46 - which, using the sine rule as described above with my diagram 1 and the angle of y which I obtain in this diagram, does not give, whereas using the sine rule in the way I described above, applied to my diagram 2 does give.

Thanks alot.

 

[LCKurtz]

The bearing is 243.8 degrees, S(52.8)W, the ground speed is 632.46 - which, using the sine rule as described above with my diagram 1 and the angle of y which I obtain in this diagram, does not give, whereas using the sine rule in the way I described above, applied to my diagram 2 does give.

Thanks alot.

But diagram 2 is not relevant to the problem, and 243.8 degrees is wrong. You can check my answer is correct by adding the plane vector 600 at 217.18 degrees to the wind 90 at 290 degrees and see that it heads southwest with length 632.46, to within roundoff errors.

 

[binbagsss]

But diagram 2 is not relevant to the problem, and 243.8 degrees is wrong. You can check my answer is correct by adding the plane vector 600 at 217.18 degrees to the wind 90 at 290 degrees and see that it heads southwest with length 632.46, to within roundoff errors.

This was the answer in the book. I assume you re correct however, may I ask how you obtained this bearing in terms of angles x and y? thanks.

 

[LCKurtz]

When you calculated $x$ in post #3 and got $x = \frac {90}{600}\sin(65)$, that should be $\sin x = \frac {90}{600}\sin(65)$ so $x=\arcsin(\frac {90}{600}\sin(65))=7.81$. If you redraw your figure with the plane, wind, and resultant velocity vector all with their tails at the origin and draw the whole parallelogram, you will see that the plane's bearing is $270-45-x=217.18$.

 

[binbagsss]

When you calculated $x$ in post #3 and got $x = \frac {90}{600}\sin(65)$, that should be $\sin x = \frac {90}{600}\sin(65)$ so $x=\arcsin(\frac {90}{600}\sin(65))=7.81$. If you redraw your figure with the plane, wind, and resultant velocity vector all with their tails at the origin and draw the whole parallelogram, you will see that the plane's bearing is $270-45-x=217.18$.

The actual calculation I did, apologies typing error, was sin x. I did obtain 7.81.
From this then when I follow the sine rule through in diagram 1 , y = 57.2, whereas in diagram 2 y = 107.19, and this leads me to different plane speeds :

Va/ sin y = 600/sin 115 or Va/siny = 600/sin 65

Thanks.

 

[LCKurtz]

The actual calculation I did, apologies typing error, was sin x. I did obtain 7.81.
From this then when I follow the sine rule through in diagram 1 , y = 57.2, whereas in diagram 2 y = 107.19, and this leads me to different plane speeds :

Va/ sin y = 600/sin 115 or Va/siny = 600/sin 65

Thanks.

Why do you keep talking about what you get when you use diagram 2? Diagram 2 is incorrect for this problem. How many times do I have to repeat that before it sinks in?

 

[binbagsss]

Why do you keep talking about what you get when you use diagram 2? Diagram 2 is incorrect for this problem. How many times do I have to repeat that before it sinks in?

Because diagram 2 leads me to deduce the value of y corresponding to the correct value of V, whereas diagram 1 corresponds to the incorrect value of y.

 

[LCKurtz]

Because diagram 2 leads me to deduce the value of y corresponding to the correct value of V, whereas diagram 1 corresponds to the incorrect value of y.

Diagram 1 gives $y = 180-65-7.81 =107.19$ which is correct for $y$.

 

[binbagsss]

Diagram 1 gives $y = 180-65-7.81 =107.19$ which is correct for $y$.

Apolgoies my diagram referencing isn't too clear, however it says that diagram 2 corresponds to the one in which I reversed the direction of VW. Diagram 2 has an angle of 65- leading to what you have said above, but diagram 1 has the angle of 115

 

[LCKurtz]

Apolgoies my diagram referencing isn't too clear, however it says that diagram 2 corresponds to the one in which I reversed the direction of VW. Diagram 2 has an angle of 65- leading to what you have said above, but diagram 1 has the angle of 115

If you refer to diagram 2 one more time I will abandon this thread. Have you verified, understood, and do you agree with my posts #8 and #12? They lead to the correct answer.

 

[binbagsss]

If you refer to diagram 2 one more time I will abandon this thread. Have you verified, understood, and do you agree with my posts #8 and #12? They lead to the correct answer.

May I ask then what the fundamental errors are with diagram 2 - in what way does the positioning of the vectors in these diagrams make one correct and the other incorrect?

 

[LCKurtz]

I am trying to lead you to the correct solution. Until you address my posts #8 and #12 either by understanding them or having questions about them, we have nothing to talk about.