Cosine theorem and maclaurin expansion

[Telemachus]

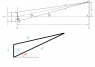
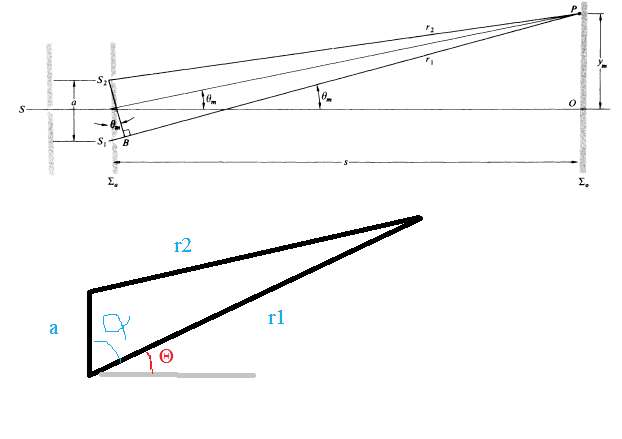
Hi. I have a doubt about an exercise in a book of optics. It's about Youngs double slit experiment. The exercise asks to apply the law of cosines. That part was easy, you can see in the diagram, alpha is the complementary angle for theta, it goes straight forward.

What I got is this expresion:

$\frac{r_2}{r_1}=\left (1-\frac{2a}{r_1}\sin \theta+\frac{a^2}{r_1^2}\right )^{1/2}$

This is in agreement with the book.

But then the book asks to make a Mac Laurin expansion for this expresion. And the thing is I don't realize what is the argument for the expansion, the book gets:

$r_2=r_1-a\sin \theta+\frac{a^2}{2r_1}\cos^2 \theta+...$

I don't know how the books gets that. At first I thought the argument was theta, but when I tried the expansion I got something more involved than that. I've tried the expansion for $\frac{r_2}{r_1}$

$\left ( \frac{r_2}{r_1} \right )_{=0}=\left (1+ \left (\frac{a}{r_1}\right )^2 \right )^2$

The first derivative:

$\left ( \frac{d\frac{r_1}{r_2}}{d\theta}\right )_0 =-\frac{a}{(r_1^2+a^2)^{1/2}}$

Then I thought of using $a/r_1$ as the argument, which is approx zero in the far field, but I think that would give pure sines in the expansion.

Help please.

 

[vela]

The book's expanding in powers of $a/r_1$. To get the second-order term correctly, you can't drop the quadratic term inside the parentheses before expanding, which is what you seem to be doing.

 

[Telemachus]

Thank you!