- #1
BMcC
- 32
- 0
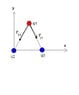
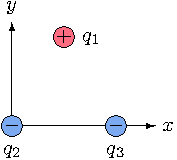
Three charged particles are placed at the corners of an equilateral triangle of side L = 1.74 m.
The charges are q1 = 3.63 µC, q2 = −8.05 µC, and q3 = −6.31 µC. Calculate the magnitude and direction (counterclockwise from the positive x axis) of the net force on q1 due to the other two charges.
First, I converted the charges from µC to C
q1 = 3.63e-6 C
q2 = -8.05e-6 C
q3 = -6.31e-6 C
Then I used Coulomb's law to figure out the forces on q1 from the other 2 charges
F21 = the force applied to charge 1 by charge 2
F31 = the force applied to charge 1 by charge 3
r = the distance between each charge = 1.74m
F21 = K*q1*q2 / r2
= (8.998e9)(3.63e-6)(-8.05e-6) / 1.742
= -0.0868 N
F31 = (8.998e9)(3.63e-6)(-6.31e-6) / 1.742
= -0.0681 N
Now because these forces applied are on the diagonal of that equilateral triangle, I must find the x and y components of the forces. The angle inside any equilateral triangle is 60 degrees, so I'm using 60 for my trig here.
x
(-0.0868 * cos60) + (-0.0681 * cos60) = -0.0774 N
y
(-0.0868 * sin60) + (-0.0681 * sin60) = -0.134 N
To find the magnitude, I've been adding the square of the x and y component, then taking the square root of it.
sqrt[(-0.0774 N)2 + (-0.134 N)2] = 0.155 N
I'm not sure if this is correct, nor am I sure how to get the direction in degrees. This method of finding the force makes sense to me but I need to submit both the magnitude and direction at the same time to get the answer correct.
Please help!
The charges are q1 = 3.63 µC, q2 = −8.05 µC, and q3 = −6.31 µC. Calculate the magnitude and direction (counterclockwise from the positive x axis) of the net force on q1 due to the other two charges.
First, I converted the charges from µC to C
q1 = 3.63e-6 C
q2 = -8.05e-6 C
q3 = -6.31e-6 C
Then I used Coulomb's law to figure out the forces on q1 from the other 2 charges
F21 = the force applied to charge 1 by charge 2
F31 = the force applied to charge 1 by charge 3
r = the distance between each charge = 1.74m
F21 = K*q1*q2 / r2
= (8.998e9)(3.63e-6)(-8.05e-6) / 1.742
= -0.0868 N
F31 = (8.998e9)(3.63e-6)(-6.31e-6) / 1.742
= -0.0681 N
Now because these forces applied are on the diagonal of that equilateral triangle, I must find the x and y components of the forces. The angle inside any equilateral triangle is 60 degrees, so I'm using 60 for my trig here.
x
(-0.0868 * cos60) + (-0.0681 * cos60) = -0.0774 N
y
(-0.0868 * sin60) + (-0.0681 * sin60) = -0.134 N
To find the magnitude, I've been adding the square of the x and y component, then taking the square root of it.
sqrt[(-0.0774 N)2 + (-0.134 N)2] = 0.155 N
I'm not sure if this is correct, nor am I sure how to get the direction in degrees. This method of finding the force makes sense to me but I need to submit both the magnitude and direction at the same time to get the answer correct.
Please help!