Counting Distinct Poker Hands with Specific Criteria

[WiFO215]

Homework Statement

A poker hand contains five cards dealt from a deck of 52. How many distinct poker hands can be dealt containing:
a) two pairs (for example 2 kings, 2 aces, and a 3)
b) a flush (five cards in a given suit)
c) a straight flush (any five in sequence in a given suit, but not including ten, jack, queen, king, ace)
d) a royal flush (ten, jack, queen, king, ace in a single suit)

The Attempt at a Solution

Essentially, I am asked to form distinct 5 tuples with certain criteria.

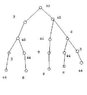
a) I've made a tree. Please tell me if there is a simpler way. Each (dot) on the tree tells you how many choices you can make at that given point. Whenever the tree branches, it goes into the various choices you can make.

For the other solutions also, I've made similar trees, but I feel this a long way. Does anyone have any other shorter methods?

 

[slider142]

For a), simplify the problem first, then use the fundamental principles of counting. How many hands are there with two kings? How many with two like cards of any type?

 

[WiFO215]

There are 4 choices for the first king and 3 for the second. Totally 12 choices for each pair. Right? And since there are 13 types of cards, I can form 13.12 pairs of cards. Is this correct? For forming a second pair, Now that one has gone, we have 12 types unused and one pair that has been used. So altogether we have 12.12 + 2 ways of forming the second pair. Adding this to the old amount, we have 25.12 + 2 ways of forming the hand. Is this correct?

 

[WiFO215]

Can anyone assist please?