- #1
George Keeling
Gold Member
- 173
- 41
Homework Statement
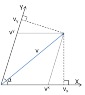
I am studying co- and contra- variant vectors and I found the video at youtube.com/watch?v=8vBfTyBPu-4 very useful. It discusses the slanted coordinate system above where the X, Y axes are at an angle of α. One can get the components of v either by dropping perpendiculars to the axes (vi) or by dropping a line parallel to the other axis (vi). These give correct results for the norm vivi and the dot product vi wi. (I have not shown w). So the vi are called contravariant and the vi are called covariant. According to the video Dirac thought this was a great example.
But both vi and vi contra-vary with a change of scale of the basis vectors. This contradicts some definitions of contravariant and covariant components, e.g. this one on Wikipedia. These definitions say that covariant components co-vary with a change of scale.
Is there a simple resolution to this apparent contradiction?
Homework Equations
Norm and dot product were calculated by expressing vi and vi in Cartesian coordinates. Quite a lot of equations! Along the way we found the metric for the slanted coordinate system.
The Attempt at a Solution
We can demonstrate the problem by drawing basis vectors on the diagram and then another set double their size.