Creating Functions from Graphs: Is It Possible?

[roppie]

Hi,

i'm not a mathematician at all so I'm sorry for not using correct jargon.



I need to create functions that give a specified output. I'm able to draw the graphs that should correspond with the output values of the function, however I haven't got a clue how to get the corresponding function...

The functions I need to create produce a single value from a single parameter. The parameter specifies a date or a number of days from a starting point.

A very good example:
I need a function that gives the percentage of extra protein need during a workout program.
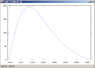
This graph (http://www.vspop.org/images/graph09.jpg" ) shows a nice example of a graph that i can produce. What is tells is that during the first days of the workout program, the percentage should gradually be increased. After a certain maximum value, the percentage should gradually drop to zero again...


Is there a way to get a function from a graph? Or is there special software available which takes this reversed approach?

Thank you all.

 

[arildno]

Is there a way to get a function from a graph?

As a nice, neat formula? Nope.

 

[roppie]

As a nice, neat formula? Nope.

No, a way

 

[CRGreathouse]

Or is there special software available which takes this reversed approach?

There's Excel and http://www.ebicom.net/~dhyams/cmain.htm.

 

[roppie]

So, if I'm correct (see attachment):

1.) I fill in the numbers
2.) I do the Curve Finder
3.) I see my function

Or do I need to be a little bit more experienced with math before I do these kind of things?

 

[CRGreathouse]

Yeah, that's pretty much it. Now choosing between some type of curve fit (on the Apply Fit menu or with the Curve Finder) and some kind of interpolation (on the Interpolate menu) depends on what you want to do, and deciding which of the curve fits is best for you also relies on what you need.

If you need any help on that, I trust you'll ask here or elsewhere?

 

[roppie]

Thank you, this is exactly what I needed

This is kinda for a secret project.. but are there any nutritional experts here?

 

[Mk]

On determining equations for graphs, if you study properties of functions for long enough, you could probably guess a function to generally describe your curve. For example, what you described might be described as a third degree polynomial with a domain and range (in the x and y values) of ≥0.

This is kinda for a secret project.. but are there any nutritional experts here?

Go ahead and visit the Biology or Medical section
https://www.physicsforums.com/forumdisplay.php?f=82
https://www.physicsforums.com/forumdisplay.php?f=149

Good luck!

I need a function that gives the percentage of extra protein need during a workout program.

Your sample graph was titled "excess deaths!" I hope you're not working them too hard.
http://www.vspop.org/images/graph09.jpg

 

[roppie]

On determining equations for graphs, if you study properties of functions for long enough, you could probably guess a function to generally describe your curve. For example, what you described might be described as a third degree polynomial with a domain and range (in the x and y values) of ≥0.

I think this will take some time lol. I imagine that after defining some functions with the help of CurveExpert, I could guess the function i should use, and maybe approximate the coefficients. For now I think I have to stick to the program..

Your sample graph was titled "excess deaths!" I hope you're not working them too hard.
http://www.vspop.org/images/graph09.jpg

I included the sample graph solely for its curve...

 

[uart]

Ropie, try the following and see if it's close enough.

y = 8.75 \, x^{1.6} \, e^{-x/12} \, - \, 16.5 \, x/74

Where x is the number of years after 2008.

 

[roppie]

Ropie, try the following and see if it's close enough.

y = 8.75 \, x^{1.6} \, e^{-x/12} \, - \, 16.5 \, x/74

Where x is the number of years after 2008.

Lol uart,

thank you for the input, but you didn't really get the question...

The curve that I attached was just an example. I need to get functions of a lot of curves... I can get them with CurveExpert...

 

[uart]

Lol uart,

thank you for the input, but you didn't really get the question...

The curve that I attached was just an example. I need to get functions of a lot of curves... I can get them with CurveExpert...

Yes I posted that as an example to see if it was close enough for your puroses because it was obtained with only some very simple parameter fitting to the general curve x^a e^{-bx}.

My point is that if your other curves are of a similar nature to the example you linked then I'd recommened experimenting with functions of this form. :)

 

[roppie]

Yes I posted that as an example to see if it was close enough for your puroses because it was obtained with only some very simple parameter fitting to the general curve x^a e^{-bx}.

My point is that if your other curves are of a similar nature to the example you linked then I'd recommened experimenting with functions of this form. :)

Sorry my bad.

I do not have a good view of how all curves will look, so i just really need a general way to get 'a function from a curve'. I'm not experienced enough to look at functions and quickly see which parameter to change, or which parameter to add/subtract to get a specific result... But thanks for the input!

 

[Focus]

I recommend that you get to know functions, more importantly distirbution shapes well. This can help you fit functions to your graphs. For example, the picture you have looks like a Weibull to me f(x) = {k \over \lambda} \left({x \over \lambda}\right)^{k-1} e^{-(x/\lambda)^k}\. You can fit the parameters using a fitting method such as least sqaures, http://en.wikipedia.org/wiki/Least_squares . Then you may wish to check the goodness of fit using chi-squared goodness of fit. http://en.wikipedia.org/wiki/Pearson's_chi-square_test

Hope this helps

 

[roppie]

I recommend that you get to know functions, more importantly distirbution shapes well. This can help you fit functions to your graphs. For example, the picture you have looks like a Weibull to me f(x) = {k \over \lambda} \left({x \over \lambda}\right)^{k-1} e^{-(x/\lambda)^k}\. You can fit the parameters using a fitting method such as least sqaures, http://en.wikipedia.org/wiki/Least_squares . Then you may wish to check the goodness of fit using chi-squared goodness of fit. http://en.wikipedia.org/wiki/Pearson's_chi-square_test

Hope this helps

Wow, it's all very logical to read. Especially about the sum of residuals which needs to has the lowest value to get the most optimal fit.

I have a very good skill of thinking conceptually and visualizing data and models, but I have very little functional knowledge of math operators etc. This makes a wiki page like the Least Squares, with a lot of Math symbols a bit overwhelming and hard to read.

Anyway thanks for the input!

p.s. Is this curve fitting method that you explain the same method that CurveFinder applies?

 

[ice109]

this is silly , you're arbitrarily modeling some kind of nutritional theory using polynomials. that's not how data modeling works. if it were that easy all theoretical scientists would just use excel.

for example here is a function i fit to real radioactive decay data using curve expert.

very pretty and smooth except that it's completely wrong outside the first and last data points because the behavior is actually similar to an exponential decay function.

so what is this secret project? scheming to sell people a workout routine based on poorly motivated models and pretty graphs?

 

[roppie]

this is silly , you're arbitrarily modeling some kind of nutritional theory using polynomials. that's not how data modeling works. if it were that easy all theoretical scientists would just use excel.

I'm not modeling, just getting the function from a curve.

for example here is a function i fit to real radioactive decay data using curve expert.

View attachment 14759

very pretty and smooth except that it's completely wrong outside the first and last data points because the behavior is actually similar to an exponential decay function.

The range where the function delivers good values is the range I'll use. Otherwise I need another curve ;-)

so what is this secret project? scheming to sell people a workout routine based on poorly motivated models and pretty graphs?

First of all, it will be free. Second, I'm not modeling, scientists do. I just use their (scientifically motivated) data to build a curve.

 

[HallsofIvy]

There are a number of ways of "curve fitting", many of which have already been mentioned. But all of them require some 'a priori' decision as to what kind of function you want to use. Given any finite amount of information, there exist an infinite number of different functions that will match that information.

 

[roppie]

There are a number of ways of "curve fitting", many of which have already been mentioned. But all of them require some 'a priori' decision as to what kind of function you want to use. Given any finite amount of information, there exist an infinite number of different functions that will match that information.

Ah , I think that is what most people here were trying to say?

As for my project, i don't think it really matters which function is used, as long as the right value is produced with given parameters...

In addition: are all different kinds of functions included in CurveExpert?

 

[uart]

this is silly , you're arbitrarily modeling some kind of nutritional theory using polynomials. that's not how data modeling works. if it were that easy all theoretical scientists would just use excel.

for example here is a function i fit to real radioactive decay data using curve expert.

View attachment 14759

very pretty and smooth except that it's completely wrong outside the first and last data points because the behavior is actually similar to an exponential decay function.

so what is this secret project? scheming to sell people a workout routine based on poorly motivated models and pretty graphs?

To be fair to the OP, hasn't mentioned anything about using the function to extrapolate the data. I agree that it would be interesting to know exactly what it will be used for.

 

[CRGreathouse]

As for my project, i don't think it really matters which function is used, as long as the right value is produced with given parameters...

In addition: are all different kinds of functions included in CurveExpert?

Many kinds of functions are included in CurveExpert, but by no means all.

The truth or falsity of your first statement quoted here depends on the application you have for your data, which you've been keeping secret. I suspect that a spline interpolation would better suit your needs...

 

[Focus]

Wow, it's all very logical to read. Especially about the sum of residuals which needs to has the lowest value to get the most optimal fit.

I have a very good skill of thinking conceptually and visualizing data and models, but I have very little functional knowledge of math operators etc. This makes a wiki page like the Least Squares, with a lot of Math symbols a bit overwhelming and hard to read.

Anyway thanks for the input!

p.s. Is this curve fitting method that you explain the same method that CurveFinder applies?

If you want an applied version, get R from http://www.r-project.org/ . Get your data on it in the form of a matrix/vector by using dat=scan("filename.txt"). Then create a function f as
f= function(x,k,lam) (k/lam)*(x/lam)^(k-1)*exp(-(x/lam)^k)

Now depending on how you sampled x you should construct a new function like this (I assume you sampled using 1 intervals)

g=function(x){
val=0
for(i in 1:length(dat)){
val=f(i,x[1],x[2])-dat
}
return(val)
}


Now if you run nlm which is a non linear minimiser with some start parameters, say 1 and 1 like this

nlm(g,c(1,1))

It should output the estimates for the parameters k and lambda. You can do the same processes with a different f in exactly the same way. It would be a bit more helpful if you did actually post the graph you have. Don't think anyone will steal it here, mathematicians are quite bad understanding real life :P

 

[gmax137]

I see this all the time - curve fitting with excel etc without considering that the form of the curve needs to match the physical process being graphed. I had a guy tell me it "must be right, the R is 0.9999999 and that can't be chance..." So I plotted it out further and asked him what the big polynomial "kink" was all about...

Sorry, this is one of my pet peeves.

 

[symbolipoint]

WHAT? Explain this or explain this better, rephrase:

I see this all the time - curve fitting with excel etc without considering that the form of the curve needs to match the physical process being graphed. I had a guy tell me it "must be right, the R is 0.9999999 and that can't be chance..." So I plotted it out further and asked him what the big polynomial "kink" was all about...

Sorry, this is one of my pet peeves.

The first part of the first sentence seems understandable, but then everything else is obscure.

 

[CRGreathouse]

gmax137 is describing someone who had fit a (high-degree) polynomial to a dataset. The data fit the polynomial very closely -- the R-value (closer to 1 is a better fit), which might typically be .995, was .99999999 or so. But just because the polynomial fit those points didn't mean the polynomial fit the actual phenomenon well. gmax137 uses the example of a 'kink' in the (extrapolated?) data, which is typical of fit polynomials: they tend to 'swing around' a bit to fit the data, and outside of the particular points you chose they may not fit well.

 

[symbolipoint]

Thanks for explaining, CRGreathouse. More clearly, data guesses are much better if a point within the extreme range are tried; outside the range - risky.

 

[gmax137]

Yes, CRGreathouse's reply clarifies what I was trying to describe. I'm sorry it I was obscure. The misunderstanding about the meaning of the "R-squared" value is what I was really trying to communicate. This value tells you how close the "predicted" values are to the given data (look up "coefficient of determination" in wikipedia). Some people (my associate included) consider a good R-squared (very close to 1.00) to mean they have selected the appropriate function to use for the curve fit. In reality, this value has no such meaning.

Now as far as my reference to the "polynomial kink" - sorry for that. If you plot out some polynomials (say x^2, then x^3, then x^4, etc) you will see that they have local maximum and minimum values (where the slope goes to zero). This is what I meant by "kink."

The ultimate point is that using a function (polynomial or otherwise) to fit data that does not follow the selected function will give erroneous results outside the range of the data used to make the fit - no matter how good the R-squared value is. And the erroneous results can be wildly off, even if you are extrapolating just a little bit beyond the range.

 

[CRGreathouse]

Now as far as my reference to the "polynomial kink" - sorry for that. If you plot out some polynomials (say x^2, then x^3, then x^4, etc) you will see that they have local maximum and minimum values (where the slope goes to zero). This is what I meant by "kink."

Actually I thought that 'polynomial "kink"' was very descriptive.

The ultimate point is that using a function (polynomial or otherwise) to fit data that does not follow the selected function will give erroneous results outside the range of the data used to make the fit - no matter how good the R-squared value is. And the erroneous results can be wildly off, even if you are extrapolating just a little bit beyond the range.

Yes, and even interpolation can be wildly off if the degree of the polynomial is too close to the number of data points. You can get wild swings as the polynomial tries to hit everything.

 

[symbolipoint]

gmax137, your re-explanation about the R and the kinks around data points also helps. The R value is best suited for statistics when you do not yet understand the mechanism which gave the counted or measured data (my guess, since I only studied statistics for a few weeks some years ago). When learning to use CurveExpert, I saw those sections of curves which deviated from actual data points which you describe. Change of curve trends too high or too low were obvious, since you could see that the data should suggest either much more or much less change.