smoics
- 28
- 0
curent and ohm's law--potential difference
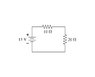
What is the potential difference across the 10 ohm resistor in the figure ?
What is the potential difference across the 20 ohm resistor in the figure?
The two resistors are in parallel and there is a battery that is 15 V.
V=IR
I think it should be relatively straightfoward, but I can't figure out how to solve for I so that I can solve for V.
Homework Statement
What is the potential difference across the 10 ohm resistor in the figure ?
What is the potential difference across the 20 ohm resistor in the figure?
The two resistors are in parallel and there is a battery that is 15 V.
Homework Equations
V=IR
The Attempt at a Solution
I think it should be relatively straightfoward, but I can't figure out how to solve for I so that I can solve for V.