- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
In summary, the conversation discusses the incorrect concepts and definitions surrounding division and the use of empty sets in mathematical operations. The speaker, Ferman, argues that the current understanding of division is erroneous and suggests a new mapping function called "D" to correctly define division. The conversation also touches on the importance of considering the number of empty sets being operated on, rather than just the result of their component elements. Ferman also presents a drawing to further illustrate their point and concludes that the use of indetermination principles in mathematical operations is not correct."
Mathematics news on Phys.org
- #2
HallsofIvy
Science Advisor
Homework Helper
- 42,989
- 975
Calling them symbols does not make nonsense anything but nonsense!
[tex]\frac{0}{0}[/tex] is NOT 1, it is not defined at all .
[tex]\frac{\infty}{\infty}[/tex] is NOT 1, it is not defined at all.
[tex]\frac{0}{0}[/tex] is NOT 1, it is not defined at all .
[tex]\frac{\infty}{\infty}[/tex] is NOT 1, it is not defined at all.
- #3
ferman
- 20
- 0
Well, perhaps is time to change erronous concepts.
"Any element divided by itself gives us the unit 1". If not, these elements aren't equal or equivalent.
It is not correct to explain properties of division with properties of multiplication, we have to do with properties of division.
"Any element divided by itself gives us the unit 1". If not, these elements aren't equal or equivalent.
It is not correct to explain properties of division with properties of multiplication, we have to do with properties of division.
- #4
cristo
Staff Emeritus
Science Advisor
- 8,146
- 74
ferman said:Well, perhaps is time to change erronous concepts.
"Any element divided by itself gives us the unit 1". If not, these elements aren't equal or equivalent.
It is not correct to explain properties of division with properties of multiplication, we have to do with properties of division.
You need to look up the definition of division. It's defined for real numbers a,b and c, as a/b=c iff a=bc and b!=0.
- #5
HallsofIvy
Science Advisor
Homework Helper
- 42,989
- 975
Yes, let's please change that erroneous concept:
"Any element divided by itself gives us the unit 1" is an erroneous concept. Please change it!
"It is not correct to explain properties of division with properties of multiplication, we have to do with properties of division."
Because you SAY so? Perhaps you should explain what YOUR definition of "division" is.
(Dang, Cristo got in just ahead of me!)
"Any element divided by itself gives us the unit 1" is an erroneous concept. Please change it!
"It is not correct to explain properties of division with properties of multiplication, we have to do with properties of division."
Because you SAY so? Perhaps you should explain what YOUR definition of "division" is.
(Dang, Cristo got in just ahead of me!)
- #6
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
Okay, let us bear with ferman for a while!
We introduce a mapping from R2 to R called "D", having the basic property of
D(a,a)=1, for all a in R.
That is valid starting point.
What other properties should D have, ferman?
We introduce a mapping from R2 to R called "D", having the basic property of
D(a,a)=1, for all a in R.
That is valid starting point.
What other properties should D have, ferman?
- #7
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
To help you out, ferman:
If "*" stands for multiplication,
should we have the rule D(a,b)=a*D(1,b) for all a and b in R?
If "*" stands for multiplication,
should we have the rule D(a,b)=a*D(1,b) for all a and b in R?
- #8
Hurkyl
Staff Emeritus
Science Advisor
Gold Member
- 14,981
- 26
ferman: you can certainly define your own division symbol to have the property that x/x=1 for all x. But that does not guarantee that it has anything to do with division as used by mathematics. (In fact, it guarantees that your definition will be incompatable with most mathematical division operations)
- #9
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
For other posters:
According to ferman's website, we also have the rule
D(a,D(a,b))=b
Do we have rules like IF D(a,b)=D(a,c), THEN b=c, ferman?
According to ferman's website, we also have the rule
D(a,D(a,b))=b
Do we have rules like IF D(a,b)=D(a,c), THEN b=c, ferman?
Last edited:
- #10
ice109
- 1,714
- 6
i don't understand why people do this. attention seeking on the internet, here of all places
- #11
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
ferman:
Should we have the rule
D(a+b,c)=D(a,c)+D(b,c), that is: [tex]\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}[/tex]?
Should we have the rule
D(a+b,c)=D(a,c)+D(b,c), that is: [tex]\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}[/tex]?
- #12
ferman
- 20
- 0
Well friends, I think I am right.
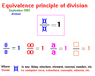
To explain my viewpoints, I put you a summary of this question with a drawing (important for comprehension). This you also can see in the end of my web, "fron zero to infinite, of ferman".
---------------
When we operate with empty sets, we usually look on (simple and exclusively) the result of their component elements to which we date as zero when having none.
But we forget something essential, and it is the number of empty sets with which we are operating.
If, as in the drawing, we take an empty glass to which we multiply by 3, the real result will be we have 3 empty glasses, but the partial result will be we have zero elements in these 3 empty glasses.
So, in this case we adjust as result ALONE THEIR ELEMENTS, but we forget we are USING A SERIES OF SETS.
Although this operation method is of great importance due to we later use this property as principle, base and justification of other operations, as can be in division.
And clear, when taking as principle and explanation to a partial result and not to the total result of the operation, because we end up accepting indetermination principles that are not correct.
For example, if we put 1x0 = 4x0 we are accepting that both terms are identical, when they are not because in the first term there is alone an empty set and the second term there are four empty sets, although the number of component elements is same in both term of the equality.
This way, when we operate (3x0 = 0) we should accept that we are operating PARTIALLY and alone with relation to the elements of the empty sets that we are using.
In the same way we should accept that this operation is PARTIALLY UNCERTAIN, since three empty sets cannot be the same thing that an empty set.
For this same reason we cannot use this type of postulates to conclude that 0/0 are an uncertain operation, since their solution is 0/0=1 abiding to the properties of the division.
To explain my viewpoints, I put you a summary of this question with a drawing (important for comprehension). This you also can see in the end of my web, "fron zero to infinite, of ferman".
---------------
When we operate with empty sets, we usually look on (simple and exclusively) the result of their component elements to which we date as zero when having none.
But we forget something essential, and it is the number of empty sets with which we are operating.
If, as in the drawing, we take an empty glass to which we multiply by 3, the real result will be we have 3 empty glasses, but the partial result will be we have zero elements in these 3 empty glasses.
So, in this case we adjust as result ALONE THEIR ELEMENTS, but we forget we are USING A SERIES OF SETS.
Although this operation method is of great importance due to we later use this property as principle, base and justification of other operations, as can be in division.
And clear, when taking as principle and explanation to a partial result and not to the total result of the operation, because we end up accepting indetermination principles that are not correct.
For example, if we put 1x0 = 4x0 we are accepting that both terms are identical, when they are not because in the first term there is alone an empty set and the second term there are four empty sets, although the number of component elements is same in both term of the equality.
This way, when we operate (3x0 = 0) we should accept that we are operating PARTIALLY and alone with relation to the elements of the empty sets that we are using.
In the same way we should accept that this operation is PARTIALLY UNCERTAIN, since three empty sets cannot be the same thing that an empty set.
For this same reason we cannot use this type of postulates to conclude that 0/0 are an uncertain operation, since their solution is 0/0=1 abiding to the properties of the division.
Attachments
- #13
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
ferman said:Well friends, I think I am right.
To explain my viewpoints, I put you a summary of this question with a drawing (important for comprehension). This you also can see in the end of my web, "fron zero to infinite, of ferman".
---------------
When we operate with empty sets, we usually look on (simple and exclusively) the result of their component elements to which we date as zero when having none.
But we forget something essential, and it is the number of empty sets with which we are operating.
If, as in the drawing, we take an empty glass to which we multiply by 3, the real result will be we have 3 empty glasses, but the partial result will be we have zero elements in these 3 empty glasses.
So, in this case we adjust as result ALONE THEIR ELEMENTS, but we forget we are USING A SERIES OF SETS.
Although this operation method is of great importance due to we later use this property as principle, base and justification of other operations, as can be in division.
And clear, when taking as principle and explanation to a partial result and not to the total result of the operation, because we end up accepting indetermination principles that are not correct.
For example, if we put 1x0 = 4x0 we are accepting that both terms are identical, when they are not because in the first term there is alone an empty set and the second term there are four empty sets, although the number of component elements is same in both term of the equality.
This way, when we operate (3x0 = 0) we should accept that we are operating PARTIALLY and alone with relation to the elements of the empty sets that we are using.
In the same way we should accept that this operation is PARTIALLY UNCERTAIN, since three empty sets cannot be the same thing that an empty set.
For this same reason we cannot use this type of postulates to conclude that 0/0 are an uncertain operation, since their solution is 0/0=1 abiding to the properties of the division.
Just a load of blather.
I have asked you several specific questions as to how your "division" interacts with other arithmetic operations, now start answering them.
- #14
ferman
- 20
- 0
Well, this would be the main property of division:
Equivalence principle:
"In any division the dividend contains N times to the quotient, being N the divider."
In this sense, the current conclusion as for 0/0 is uncertain, and so any number could be the result of this division seen to be clearly incorrect. Question that we can see with any example:
If were 0/0 = 7 then we would have that the dividend ( 0 ) should be seven times superior than the divider ( also 0 ) and this is not this way since they are the same one.
Equivalence principle:
"In any division the dividend contains N times to the quotient, being N the divider."
In this sense, the current conclusion as for 0/0 is uncertain, and so any number could be the result of this division seen to be clearly incorrect. Question that we can see with any example:
If were 0/0 = 7 then we would have that the dividend ( 0 ) should be seven times superior than the divider ( also 0 ) and this is not this way since they are the same one.
- #15
ferman
- 20
- 0
Don't worry, I'll treat to response all them. Time to do.
- #16
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
Again, mere silly blather about "correctness".ferman said:Well, this would be the main property of division:
Equivalence principle:
"In any division the dividend contains N times to the quotient, being N the divider."
In this sense, the current conclusion as for 0/0 is uncertain, and so any number could be the result of this division seen to be clearly incorrect. Question that we can see with any example:
If were 0/0 = 7 then we would have that the dividend ( 0 ) should be seven times superior than the divider ( also 0 ) and this is not this way since they are the same one.
I have already taken into account your desire to have a "D" mapping satisfying the basic principle D(a,a)=1 for all a in R.
What of the other properties I've mentioned does D have?
- #17
HallsofIvy
Science Advisor
Homework Helper
- 42,989
- 975
Doesn't this contradict what you initially said, "It is not correct to explain properties of division with properties of multiplication, we have to do with properties of division" since you are now DEFINING division in terms of multiplication?ferman said:Well, this would be the main property of division:
Equivalence principle:
"In any division the dividend contains N times to the quotient, being N the divider."
Now, you are going to have to tell us what you mean by "seven times superior than the divider". I don't believe "superior" is standard mathematics notation.In this sense, the current conclusion as for 0/0 is uncertain, and so any number could be the result of this division seen to be clearly incorrect. Question that we can see with any example:
If were 0/0 = 7 then we would have that the dividend ( 0 ) should be seven times superior than the divider ( also 0 ) and this is not this way since they are the same one.
While I might be getting lost in the grammatical intricacies of "so any number could be the result of this division seen to be clearly incorrect" (isn't there a verb missing from this clause?), if I am interpreting this correctly you seem to be now agreeing with what I said and contradicting the assertion on your website that 0/0= 1.
- #18
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
Besides, 0=0+0+0+0+0+0+0=7*0, that is, 0 IS 7 times "superior" than itself..
- #19
ferman
- 20
- 0
Well, perhaps I find very complicated some of your questions.
My rule or main property of division is very easy:
Given a, b and c that can be any type of number (or elements) the division a/b=c is correct "when a contain b time to c".
6/3=2 6 contains 3 time to 2
8d/2=4d 8d contain 2 time to 4d
d/4 = h d contains 4 time to h
S/1 = S S contains 1 time to S
Now well, when is the same o equivalent element that is divided by the same one, we obtain the pure unit without no one type of qualification.
6/6 give us 1
0,01/0’01 give us 1
h/h give us 1
@/@ give us 1
x/x give us 1
All this propitiated by the commutive property of division (second property): " En any division we can change the dividend by the quotient being also fulfilled the new resultant equality"
6/3=2 --------- 6/2=3
S/1=S --------- S/S=1
Sorry for not understand well your other proposals.
My rule or main property of division is very easy:
Given a, b and c that can be any type of number (or elements) the division a/b=c is correct "when a contain b time to c".
6/3=2 6 contains 3 time to 2
8d/2=4d 8d contain 2 time to 4d
d/4 = h d contains 4 time to h
S/1 = S S contains 1 time to S
Now well, when is the same o equivalent element that is divided by the same one, we obtain the pure unit without no one type of qualification.
6/6 give us 1
0,01/0’01 give us 1
h/h give us 1
@/@ give us 1
x/x give us 1
All this propitiated by the commutive property of division (second property): " En any division we can change the dividend by the quotient being also fulfilled the new resultant equality"
6/3=2 --------- 6/2=3
S/1=S --------- S/S=1
Sorry for not understand well your other proposals.
- #20
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
As I have already stated, you wish D to have the property D(a,D(a,b))=b.
Fine. You are entitled to that. Now go on.
Fine. You are entitled to that. Now go on.
- #21
ferman
- 20
- 0
You say:
Besides, 0=0+0+0+0+0+0+0=7*0, that is, 0 IS 7 times "superior" than itself..
This is what now matematics say, but not what I say.
I say 0=0+0+0+0+0+0+0 is not equal. 0 = 7*0 is not equal.
Besides, 0=0+0+0+0+0+0+0=7*0, that is, 0 IS 7 times "superior" than itself..
This is what now matematics say, but not what I say.
I say 0=0+0+0+0+0+0+0 is not equal. 0 = 7*0 is not equal.
- #22
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
Okay, so you now wish to change the definition of 0 as well, not only "division".ferman said:You say:
Besides, 0=0+0+0+0+0+0+0=7*0, that is, 0 IS 7 times "superior" than itself..
This is what now matematics say, but not what I say.
I say 0=0+0+0+0+0+0+0 is not equal. 0 = 7*0 is not equal.
- #23
ferman
- 20
- 0
Thank you for listen to me.
- #24
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
ferman said:Thank you for listen to me.
It won't last long, I assure you, unless you make an effort to be intelligible.
- #25
matticus
- 107
- 1
assume 0/0 = 1. then n*(0/0) = (n*0)/0 = 0/0 = n*1 = n. so 0/0 = n, too.
- #26
ferman
- 20
- 0
When we have division by 0, 3/0, 6/0, etc. we always obtain solution we limit infinite, but when we have the division between equal values 0/0 , a/a, @/@ etc. we obtain as result the unit 1.
This is due the dividend and divider are the same, with the same value.
Then we have that uniquely when we divide 0/0 is when we obtain a determinate value, 1.
This circumstance obliges us to resolve before the question 0/0 and later resolve the other operations.
Then we can say that: the 0/0 have priority on the other operations, with object of not produce indeterminate operations as 3/0, 8/0 N/0, etc.
Then your example would be:
N*0/0 = N*1 = N
This is perfectly logical due to if we multiply a number N by other 0 and immediately we divide N by the same 0, the number N can’t change its value.
Although the current viewpoint where N*0/0 = 0/0 is not consequent with lo logic and comprehension, due to if we multiply N by 0 and divide by 0 at the same time, the value of N change to indeterminate. Not logic. Alone erroneous rules of multiplication can drive us to this conclusion.
As you can see, is the unique case (0/0) in that the division by 0 give us a determinate solution.
This is due the dividend and divider are the same, with the same value.
Then we have that uniquely when we divide 0/0 is when we obtain a determinate value, 1.
This circumstance obliges us to resolve before the question 0/0 and later resolve the other operations.
Then we can say that: the 0/0 have priority on the other operations, with object of not produce indeterminate operations as 3/0, 8/0 N/0, etc.
Then your example would be:
N*0/0 = N*1 = N
This is perfectly logical due to if we multiply a number N by other 0 and immediately we divide N by the same 0, the number N can’t change its value.
Although the current viewpoint where N*0/0 = 0/0 is not consequent with lo logic and comprehension, due to if we multiply N by 0 and divide by 0 at the same time, the value of N change to indeterminate. Not logic. Alone erroneous rules of multiplication can drive us to this conclusion.
As you can see, is the unique case (0/0) in that the division by 0 give us a determinate solution.
- #27
cristo
Staff Emeritus
Science Advisor
- 8,146
- 74
I think you should replace the "we" in your post with "I." Division by zero is undefined, as has been explained to you above, in the "usual" number systems.ferman said:When we have division by 0, 3/0, 6/0, etc. we always obtain solution we limit infinite, but when we have the division between equal values 0/0 , a/a, @/@ etc. we obtain as result the unit 1.
- #28
- #29
DeadWolfe
- 457
- 1
Out of curiousity, are you using this new concept of division to help you build a perpetual motion machine?
- #30
ferman
- 20
- 0
Well, as joke is good.
No, my intention is give worth to division as mathematic operation with its own entity and not as succedaneum of multiplication.
We have to remember that multiplication and division have different properties, so we can’t express and explain division with properties of multiplication.
This case I bet for particular properties for division as the Equivalence principle or the Commutive property.
Thank you.
No, my intention is give worth to division as mathematic operation with its own entity and not as succedaneum of multiplication.
We have to remember that multiplication and division have different properties, so we can’t express and explain division with properties of multiplication.
This case I bet for particular properties for division as the Equivalence principle or the Commutive property.
Thank you.
- #31
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
Again, I ask you:
What other properties than D(a,a)=1 and D(a,D(a,b))=b for all real a,b would you like your "division" operation to have?
What other properties than D(a,a)=1 and D(a,D(a,b))=b for all real a,b would you like your "division" operation to have?
- #32
d_leet
- 1,077
- 1
arildno said:Again, I ask you:
What other properties than D(a,a)=1 and D(a,D(a,b))=b for all real a,b would you like your "division" operation to have?
To ferman
You should note that if you also wish to have the property that 0/a is 0 for all nonzero a then the two properties that arildno mentions above are not consistent because then if we take any nonzero b we would have
D(0,b)=0
and
D(0,D(0,b))=b
BUT
since D(0,b)=0
we have that D(0,D(0,b))=D(0,0)=1
And thus if you wish to have the three properties
1). 0/a=0 for all nonzero a
2). D(a,a)=1 for all a
3). D(a,D(a,b))=b
These imply that for all nonzero b, b=1.
- #33
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,123
- 137
I was sort of waiting for him to fall into that little trap..
- #34
Moo Of Doom
- 366
- 1
d_leet said:And thus if you wish to have the three properties
1). 0/a=0 for all nonzero a
2). D(a,a)=1 for all a
3). D(a,D(a,b))=b
These imply that for all nonzero b, b=1.
I'm under the impression, that he would reject (1). He has said that N*0 = 0 is only "partially" true, and thus 0/a = 0 probably only "partially" holds. It is a bit hard to decipher his ramblings, though...
- #35
d_leet
- 1,077
- 1
Moo Of Doom said:I'm under the impression, that he would reject (1). He has said that N*0 = 0 is only "partially" true, and thus 0/a = 0 probably only "partially" holds. It is a bit hard to decipher his ramblings, though...
Yea that is probably true, but then he can't be willing to accept that a+0=0+a=a for all a anymore, so he needs to redefine the properties of zero, and of the arithmetic structure of his whole system in order to tell whether or not it is consistent with itself and what he wants it to do.
Similar threads
- Replies
- 3
- Views
- 810
-
General Math
- Replies
- 1
- Views
- 948
-
General Math
- Replies
- 1
- Views
- 738
-
Mechanical Engineering
- Replies
- 8
- Views
- 2K
-
General Math
- Replies
- 31
- Views
- 2K
-
General Math
- Replies
- 2
- Views
- 401
-
General Math
- Replies
- 15
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 8
- Views
- 1K
- Replies
- 72
- Views
- 4K
-
General Math
- Replies
- 2
- Views
- 250
Share: