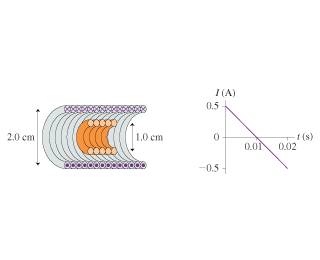
Linus Pauling said:
B for the solenoid = mu0NI/l = 9.1*10-4 if I use 0.5A for I. I am not sure if that value for I is correct... I just figured it's not zero so this seemed like a natural choice. Whether or not this is correct, can someone explain what I value is correct and why? Proceeding with the claculation:
flux per coil = B*A = 7.15*10-8 Tm2
EMF of the coil = d(flux)/dt * N = (7.15*10-8)/0.01 s * 5 turns = 3.57*10-5 V
EMF = IR
I = EMF/R = 1.79*10-4 A
Sorry for the delayed response.
I haven't gone through the whole problem myself, but I think you're getting close, but not quite.
Start with the equation for
B, like you've already done, but leave the answer in terms of
I. There's no point in sticking a specific number in for
I since
I is changing.
Next, look at the plot and come up with an equation for
dI/dt. You should be able to use that to find an expression for
dB/dt. How does that relate to -dΦ/dt in the coil? (where Φ is the flux and dΦ/dt is the rate of change of flux per unit time).
[Edit: Like I mentioned before, I haven't double checked all the math, but I just noticed that you started with I = 0.5 A, and then later divided by 0.01 s in a later part of the problem, which might end up giving you the right answer in the end (but possibly by coincidence, depending on how the grader interprets your work). If your instructor is grading on partial credit, I suggest redoing the problem in terms of
dI/dt and
dB/dt . It gives a cleaner way of getting to the solution.]
[Edit 2: Also, don't forget about the negative sign in the \epsilon = -\frac{d\Phi}{dt}, if you are required to show the direction of the induced current. (Which I'm guessing you are -- the problem statement gave a convention for what is positive current, meaning your answer might be negative, if the current flows in the opposite direction of the positive-convention.)]