Current density peaks at the interface conductor/insulator

[No_127_0_0_1]

Hello everyone,

I have a physics problem that I have been struggling with for a long time. Many many hours of searching around for theoretical or practical answers have not given me anything definitive.

The question is in the context of electrical engineering, more specifically peaks in current density at the edge between insulators and conductors.

I find peaks solving models in COMSOL multiphysics software and I have modified the geometry to remove any sharp corner to avoid singularities, but the peaks remain.

Here is the context: I am modeling ablation through a catheter. The catheter has a voltage applied.
To show it graphically, I used a simple 2D axysimmetrical model (so it is actually 3D) to check the current density in specific spots around an electrode.

Here is an image that summarizes both the geometry and the problem that I am encountering. All around the electrode and shaft, there is biological tissue.

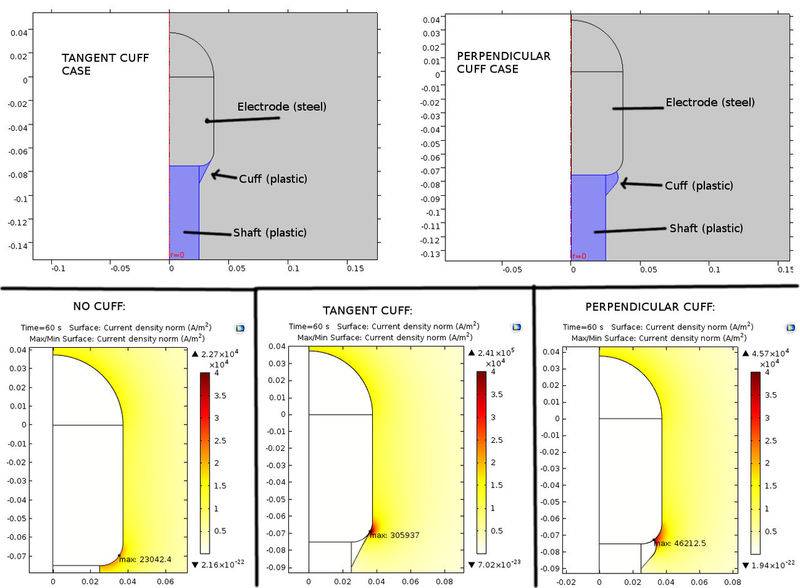
The electrode is at the end of a catheter and has a "cuff" that is made of plastic and partly covers the bottom part of the electrode (the part with the highest curvature).

In reality, in our lab-made catheters, the cuff is tangent to the electrode.
In COMSOL the results show a huge peak in the current density at the point where the cuff meets the electrode.

If I remove the cuff, there is still a higher current density in the area, since the electrode has a curvature in that area. But the peak without cuff is much smaller than the peak with cuff:

I tried changing the tangent angle, making the cuff perpendicular to the electrode. This causes a peak still, but an order to magnitude less than the tangent cuff case.

Without cuff, the max current density is 23,042 A/m^2. With tangent cuff it is 305,937 A/m^2. With perpendicular cuff it is 46,212 A/m^2

The same thing happens for a lot of other types of geometries where an insulator meets a conductor. I know there is going to be a high gradient for V when you go from insulator to conductor but it still does not explain the tiny area of sharp peak in current density.

The results make me wonder whether the peaks for both tangent and perpendicular cuff are the result of a singularity and if, in reality, there is a peak in that location or not.
If I make the mesh finer, the value of the peak in current density increases, which also makes me think of an artifact / singularity.

Now, with the tangent cuff, one could argue that if there is a singularity.
But with a perpendicular cuff, you already have an angle that is as wide as it can possibly be. So I don’t see how that can be a singularity.

So I was wondering: has anyone ever seen either in theoretical computation or in practical application that if you add an insulator that partly cover a conductive surface you have a sharp (but with small area) peak at the interface between the insulator and the conductor?

I would greatly appreciate any feedback on this.

Thank you so much in advance

Best regards

Rossana

 

[Jeff Rosenbury]

Currents do tend to concentrate near the surface. Read up on skin effect to understand why.

It helps to understand that the energy of electricity is in the magnetic and electric fields. These fields propagate near, but not in the conductors.

You might try another material with a lower (or higher) dielectric constant for your sleeve.

 

[No_127_0_0_1]

Thanks Jeff. In DC, which is what I am modeling, there would be no skin effect.
However your suggestion of trying different permittivity values made me think of a parametric study where I set different material values to different regions.
I believe I solved the problem:
The permittivity does not make any difference in such peaks. Only sigma, the electrical conductivity, does. It makes sense given that the current density J can me approximated as sigma*E and E is -grad(V).
The peaks are not an artifact but a natural consequence of the differences in sigma in combination with high grad(V) in curved areas.

Thank you :)