Find Current I1 in 7.5 Ω Resistor with Kirchhoff's Rule

  • Thread starter Thread starter deenuh20
  • Start date Start date
  • Tags Tags
    Current Resistor
AI Thread Summary
To find the current I1 through a 7.5 Ω resistor using Kirchhoff's Rule, the user attempted to calculate equivalent resistances and break down the total current into I1 and I2. Despite following the correct approach, they did not arrive at the expected answer of 0.65 A. Other participants confirmed that the method used was valid and suggested reviewing the calculations for potential errors. Sharing the detailed working steps was recommended for further assistance. Accurate application of Kirchhoff's rules is essential for solving such circuit problems effectively.
deenuh20
Messages
50
Reaction score
0

Homework Statement


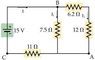
In the circuit below: (a) Find the current I1 that passes through the 7.5 Ω resistor.



Homework Equations



Kirchhoff's Rule--Loops

The Attempt at a Solution


This was a problem in my textbook. The answer is .65 A, but I don't understand how to get that. I tried Kirchhoff's rule by finding equivalent R between A & B and Then finding equivalent R between A & C then finding I, Then breaking I into I1 and I2 (according to the parallel resistances between A & B)

However, I still didn't get the answer, .65 A. Was my approach correct, or is there another way? Thank you.
 

Attachments

  • Circuit 2.jpg
    Circuit 2.jpg
    8.4 KB · Views: 461
Physics news on Phys.org
Your plan of how to solve it is OK, and when I did it that way I got 0.65A.

If you can't find your mistake, show your working, then somebody can check through it.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Power dissipated in this circuit with 2 batteries and 3 resistors
Replies
22
Views
4K
Kirchhoff's law: Find the current I3 through the Amp meter
Replies
4
Views
2K
Sign conventions for Kirchhoff's loop rule
Replies
7
Views
1K
Finding the currents in this circuit (2 voltage sources and 3 resistors)
Replies
10
Views
2K
How to solve this chain with Kirchhoff's laws?
Replies
18
Views
3K
Using Kirchhoff's Rule - Theory question
Replies
8
Views
2K
What is the current through each resistor in this circuit?
Replies
3
Views
4K
Solving Current & Power in 4 & 3 Wire Circuits
Replies
9
Views
2K
Circuit analysis: Six resistors and two batteries
Replies
1
Views
2K
Find currents I1 and I2 in a 3-loop, 2-battery circuit
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top