dancergirlie
- 194
- 0
Homework Statement
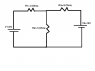
Find the current through R2 (see attached figure)
Homework Equations
The Attempt at a Solution
Not really sure if I did this right, would like if someone would double check my work:
First I tried Using Kirchhoff equations for a node and I got:
I1-I2+I3=0
Next I broke it down into two loops using the fact that the voltage drops across a closed loop is zero:
Loop 1: V1-3*I1-5*I2=0
Loop 2: V2-8*I3-5*I2=0
Using the second equation I got:
8*I3=V2-5*I2
I3=(V2-5*I2)/8
Next, plugging that into the Kirchhoff equation, I can solve for I1 in terms of I2:
I1=I2+(5*I2-v2)/8=(13*I2)/8
Lastly, plugging the values for I1 and I3 into the loop 1 equation, I get:
V1=3((13*I2-V2)/8)+5*I2
V1=(39*I2-3*V2)/8 + (40*I2)/8= (79*I2-45)/8
Using V1=5:
40=79*I2-45
85=79*I2
I2=1.08A
I am not confident in that answer though :/
Any help would be great!
Attachments
Last edited: