Current, Power and Energy in an Inductance

[dudforreal]

Homework Statement
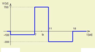
The graph below shows the voltage across a 820 mH inductor vs. time.
Find the current (Ix), the power delivered (Px) and the energy stored (Wx) at time tx = 9 μs.


The attempt at a solution

I tried adding up the areas of the rectangles up to tx and multiplying it by 820m but this gives the wrong answer for Ix.

 

[Centrus]

You are very close! Keep plodding along.

The voltage across an inductor is given by:

$V = L\dfrac{dI}{dt}$

Now, after rearranging to isolate $\dfrac{dI}{dt}$, and then integrating, what do you get? Hint: you shouldn't be multiplying the sum of the areas of the rectangles by 820mH.

Also, are you ensuring that you subtract contributions from areas beneath the $t$ axis?

 

[dudforreal]

cool...not sure on how to get voltage in order to get power

 

[dudforreal]

...and what if the area was 0 altogether?

 

[Centrus]

The question asks for the power at tx = 9 μs. I.e. it's asking for an instantaneous power, and so you only need the voltage at that point in time. This you can easily read from the graph to be 700 V.

If the voltage V = 0, then the power (at that point in time) P = VI = 0.

 

[dudforreal]

cool got the answer thanks for the help

 

[Centrus]

No worries!