Current problem with emf and internal resistance

[jamesbiomed]

Homework Statement

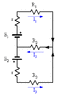
Assuming each battery has internal resistance r = 1.0 Ω, determine the magnitudes and directions of the currents through each resistor shown in the following figure. The batteries have emfs of 1 = 9.0 V and 2 = 12.0 V and the resistors have values of R1 = 15 Ω, R2 = 20 Ω, and R3 = 30 Ω.

Find Current through R1, R2, R3

PLEASE SEE PICTURE:

http://www.webassign.net/gianpse3/26-40.gif

Homework Equations

V=Emf-r*I
V=I*R

The Attempt at a Solution

When two batteries are in a series, their total voltage is the algebraic sum of of their respective voltages.

For R1: I used V=emf-r*I and set it equal to I*R. My first attempt I added the emf's and plugged into the equation and it didn't work. Then I tried adding (emf-r*I)+(emf-r*I) for both eq'ns and setting equal to I*R and was incorrect.

I tried this for all three to no avail.

Since the resistance is given for each, and I'm not adding them, the fact that they are parallel or in a series with each other was not taken into consideration. But I have been getting the feeling that maybe this should have been...

Any help would be really nice

 

[gneill]

The internal resistance of E1 is in series with R1, and the internal resistance of E2 is in series with R3. Why not "sneak" the internal resistances into the values of the corresponding resistors? In other words, add 1Ω to each of R1 and R2 and then proceed.

There are several possible ways to proceed with analysis including using KVL and KCL equations, node voltage analysis, current mesh equations, or even superpostion. What have you learned about so far?

 

[jamesbiomed]

Appreciate the reply:

Do mean "sneak" one ohm in because V=E1-rI=RI? Since r=1, to solve that you add one I to both sides...I don't think that's what you meant, so could you expand?

This is a undergraduate Physics 2 course. Are KVL eq'n's Kirchhoff's rules? The rest that you named are not familiar.

I've just learned emf, internal resistance, parallel and series circuits, batteries, etc.

 

[gneill]

Appreciate the reply:

Do mean "sneak" one ohm in because V=E1-rI=RI? Since r=1, to solve that you add one I to both sides...I don't think that's what you meant, so could you expand?

I just meant that since those resistances are in series, you can combine them. This will not affect any current values in the circuit (since current is the same for components in series).

This is a undergraduate Physics 2 course. Are KVL eq'n's Kirchhoff's rules? The rest that you named are not familiar.

Yes, KVL and KCL are Kirchhoff's Voltage and Current laws respectively. So it looks like you'll be writing KVL and KCL equations for the circuit.

I've just learned emf, internal resistance, parallel and series circuits, batteries, etc.

Okay, why not begin by labeling the currents and identifying where you'll be applying KVL and KCL?

 

[jamesbiomed]

I just meant that since those resistances are in series, you can combine them. This will not affect any current values in the circuit (since current is the same for components in series).

Ok, got it.

Yes, KVL and KCL are Kirchhoff's Voltage and Current laws respectively. So it looks like you'll be writing KVL and KCL equations for the circuit.



Okay, why not begin by labeling the currents and identifying where you'll be applying KVL and KCL?

Alright, I've labeled some values points of reference, and am treating it basically like two closed loops to get equations:

V=30I3-20I2=0
V=15I1-20I2=0

That's 2 eq'ns, three unknowns. I feel like combining R1 and R3 like you referenced earlier ^ might solve that. Am I in the right direction?

 

[gneill]

Alright, I've labeled some values points of reference, and am treating it basically like two closed loops to get equations:

V=30I3-20I2=0
V=15I1-20I2=0

That's 2 eq'ns, three unknowns. I feel like combining R1 and R3 like you referenced earlier ^ might solve that. Am I in the right direction?

When you write KVL for a loop, be sure to include any voltage sources (and pay attention to their polarity). Here you have two voltage sources, E1 and E2, one in each loop. It would be helpful to know what directions you picked to assign to the currents.

Yes, you can add in the source resistances to R1 and R3 if you wish, or write separate terms for them in the equations --- algebraically they will end up added anyways.

For a third equation you should pick a convenient node in the circuit for which you can write a KCL equation. This will then specify a relationship between the currents I1, I2, and I3.

 

[jamesbiomed]

No rush on this, I'm in EST zone so this will be my last post for tonight...

The third eq'n definitely makes sense, and there is an obvious node here to choose. Btw, I have currents running to the outside from each respective voltage source, then looping around through the middle...

I went ahead and added your suggestions and solved for I1, and still came up wrong. Can you check my methods?

-30I3+12-20I2=0
-15I1+9-20I2=0
I1+I3=I2 {The node I picked was the intersection of the two loops on the side opposite the batteries}

Solving for I1:
-30I3+12-20I2=0 gives I3=(15I1+3)/30

I1+I3=I2 and ^ can be plugged into my second eq'n,

-15I1+9-20[I1+{15I1+3}/30]=0 gives I1=11/25

 

[gneill]

I don't see terms for the internal resistances (or alternatively, the internal resistances having been added to R1 and R3). Otherwise, your equation methodology looks fine.

Your labeled circuit probably looks something like this:

 

[jamesbiomed]

I don't see terms for the internal resistances (or alternatively, the internal resistances having been added to R1 and R3). Otherwise, your equation methodology looks fine.

Excellent, this worked out well. Thank you!

Your labeled circuit probably looks something like this:

Yes, that's exactly my model.

 

[Redbelly98]

Okay. Well, let's look at one of the equations you wrote:

-30*I3 + 12 - 20*I2=0​

You left out a term to account for the voltage drop across the r=1Ω resistor. (And you also left it out of your other KVL equation.)

 

[jamesbiomed]

Redbelly, that's true, I added "1" to resitor's 1 and 3 and got the correct answer. Thanks!

 

[Redbelly98]

You're welcome, glad it worked out