eatsleep
- 42
- 0
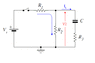
http://imgur.com/PQ4XCEo
2.V=IR
3. I know the capacitor has a voltage of 5.5 because it is charged to the supply voltage, I don't understand what happens to current when the switch is opened.
2.V=IR
3. I know the capacitor has a voltage of 5.5 because it is charged to the supply voltage, I don't understand what happens to current when the switch is opened.