nissan4l0
- 11
- 0
I am having trouble understanding the concept of cylindrical symmetry in an infinitely long line.
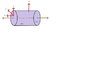
Please picture a finite Gaussian cylinder enclosing a portion of the length of the line, parallel to the line.
My book states that there cannot be any component of E perpendicular to the radius of the cylinder; the electric field lines can only be radial, that is, through the side walls, not through the end caps.
As I understand it, the line charge is composed of many individual point charges; each point charge has an electric field that spreads out in all directions radially, including perpendicular to the end caps. Why do we assume that there is no field at the end caps?
Please picture a finite Gaussian cylinder enclosing a portion of the length of the line, parallel to the line.
My book states that there cannot be any component of E perpendicular to the radius of the cylinder; the electric field lines can only be radial, that is, through the side walls, not through the end caps.
As I understand it, the line charge is composed of many individual point charges; each point charge has an electric field that spreads out in all directions radially, including perpendicular to the end caps. Why do we assume that there is no field at the end caps?