Jeff12341234
- 179
- 0
I lost the A variable when I simplified this. Did I go wrong somewhere?
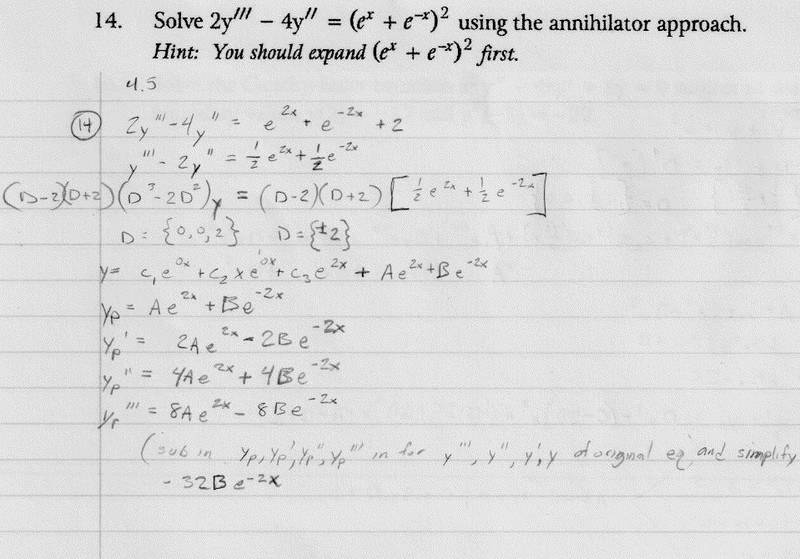
You're still not getting this - you're making the same mistakes you made in a previous post a week or so ago.Jeff12341234 said:I lost the A variable when I simplified this. Did I go wrong somewhere?
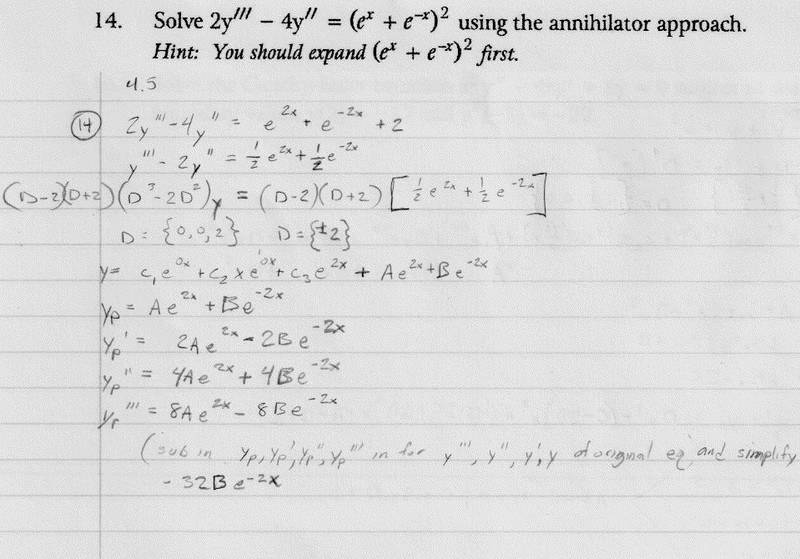
No, not quite. The general solution of your nonhomogeneous equation will be composed of six functions, which corresponds to the number of roots (six) of the characteristic equation of the sixth-order homogeneous equation.Jeff12341234 said:I ended up realizing my mistake I think. Yes, it was the same error I made before. I got:
y = c1+c2x+c3e2x+Axe2x+Be-2x
Jeff12341234 said:which resulted in a final answer of:
y = c1+c2x+c3e2x+\frac{1}{8}xe2x-\frac{1}{32}e-2x
Is that right?
Yes, it is. Speaking of images, please take some time and shrink your images so that they fit the window. The max. size should be no larger than 900 x 600. When they're wider than that, you have to scroll to see the entire image.Jeff12341234 said:Is the original image showing up?
Yes.Jeff12341234 said:Oh, I should've had a one on the right side. Simple math mistake. 2/2 does not equal 0! I did need to divide the entire thing by two didn't I?
Mark44 said:You can check it yourself, you know. You can do it in two parts.
1. Verify that D2(D - 2)[c1 + c2x +c3e2x] = 0.
2. Verify that D2(D - 2)[(1/8)xe2x - (1/4)x2 - (1/32)e-2x] = (1/2)[e2x + 2 + e-2x].
Mark44 said:You can check it yourself, you know. You can do it in two parts.
1. Verify that D2(D - 2)[c1 + c2x +c3e2x] = 0.
2. Verify that D2(D - 2)[(1/8)xe2x - (1/4)x2 - (1/32)e-2x] = (1/2)[e2x + 2 + e-2x].
Step 1 does result in 0. You are confusing multiplication with operator composition. The operator D2(D - 2) does not mean y'' * (y' - 2). If you expand D2(D - 2), you get D3 - 2D2.Jeff12341234 said:Well step one doesn't equal zero.. What did I do wrong?
if y = c1 + c2x +c3e2x
y"(y'-2) = 4c3e2x(2c3e2x+c2-2)
Almost. y''' = D3y, and y'' = D2y, so y''' - 2y'' = (D3 - 2D2)y. Note that, for example, Dy does not mean D * y, any more than ##\frac{dy}{dx}## means ## \frac{d}{dx} * y##.Jeff12341234 said:That's what I already have. It's just a one step process. You replace y''' with D3 and y'' with D2 resulting in D3-2D2.
Because of the close relationship between the operator factorization and the characteristic equation.Jeff12341234 said:What would be the point of even mentioning, or arranging it as D2(D-2)??
Using annihilators, there are three diff. equations you need to keep track of:Jeff12341234 said:I thought the test was for Yp; the D(D-2)(D+2) part.. I'm kind of confused now..
If I use Yc, as you seem to suggest, and make sure everything is expanded out, then it passes both tests. However some examples from my notes don't pass the test
?Jeff12341234 said:y"-2y'+y turns into D2-2D+1, you get c1ex+c2xex. That test doesn't pass for step one.
In operator notation, the DE above is (D2 - 2D + 1)y = x3+4x, or (D - 1)2y = x3+4x .Jeff12341234 said:Right. You basically re-explained what you already explained earlier. The point i was trying to make was that the test you said to use marks problems incorrect that were example problems given by the instructor. An example of this was:
y"-2y'+y=x3+4x
y"-2y'+y turns into D2-2D+1.
You then get yc=c1ex+c2xex.
That's all the info you need to try test one on this problem and it fails it.
Mark44 said:It should be the case that (D - 1)2(c1ex + c2xex) = 0.
It should also be the case that (D - 1)2(A + Bx + Cx2 + Dx3) = x3 + 4x.
So how do you see this failing?
Jeff12341234 said:If you set f(x)=c1ex + c2xex
and then do (\frac{d}{dx}[f(x)]-1)2 into a calc like mine then you don't get zero.
You get ((c2x+c1+c2)ex-1)2. Even if you expand (D - 1)2 out and then do it, you still don't get zero.
When using the exact same technique on the original problem that this thread was based on, you do get 0. So what's going on here?
Jeff12341234 said:If you set f(x)=c1ex + c2xex
and then do (\frac{d}{dx}[f(x)]-1)2 into a calc like mine then you don't get zero.
Aaaaah, that's the real calculation. No need for that silly D notation except for finding zeros. Yes, when you cut straight to what actually needs to be calculated, I also get zero. (ex (c1+c2 (x+2)))-2(ex (c1+c2x+c2))+(c1ex + c2xex)=0Mark44 said:Let y = c1ex + c2xex.
Calculate y' and y''.
What do you get for y'' - 2y' + y? I get 0.