kstylian
- 4
- 0
Hi All,
This is my first post here, and thanks in advance for any help and direction.
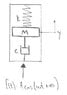
I'm trying to model an enclosed damped mass spring system with an external forcing function acting on the system (not on the mass directly). Ultimately I would like to plot/calculate the motion (y) of the mass relative to the system, supposing the forcing function is sinusoidal.
Please see attachment.
Thanks again.
This is my first post here, and thanks in advance for any help and direction.
I'm trying to model an enclosed damped mass spring system with an external forcing function acting on the system (not on the mass directly). Ultimately I would like to plot/calculate the motion (y) of the mass relative to the system, supposing the forcing function is sinusoidal.
Please see attachment.
Thanks again.