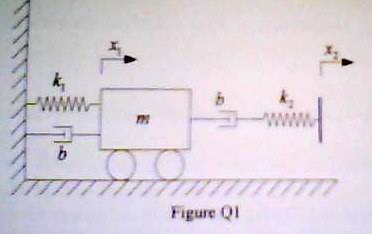
How Do You Derive the Equation for a Damper and Spring in Series?

[jackycheun]

1. Please help. How should I derive the equation for the damper and spring at right side of the mass(as shown in attach pic)? Can I combine both together as Fd + Fs or I need to have set a point between the spring and damper? Thanks.

 

[CEL]

1. Please help. How should I derive the equation for the damper and spring at right side of the mass(as shown in attach pic)? Can I combine both together as Fd + Fs or I need to have set a point between the spring and damper? Thanks.



View attachment 17877

If the damper and the spring are in series, the force applied is the same on both of them and propagates to the mass. This force will cause a change of length in the spring and a variation of the velocity in the damper.
I prefer to make an analogy with electric circuits. Force is analog to current, velocity is analog to voltage, displacement is analog to magnetic flux, mass is analog to capacitance, elastic constant is analog to the inverse of inductance and viscous friction is analog to conductance.
So, in the same way that a current in series with a resistor and an inductor will give origin to voltages Ri and L\frac{di}{dt}, the force in series with a damper and a spring will give origin to velocities \frac{1}{b}f and \frac{1}{k}\frac{df}{dt}