Decay of Alpha Particle Through Quantum Tunneling

Click For Summary
SUMMARY

The discussion centers on the emission of high-energy alpha particles by alpha-emitters with short wavelengths, specifically addressing the shape of the associated graph. The Transmission Coefficient Equation (T=exp(-2kd)) is referenced to explain the quantum tunneling phenomenon. Participants conclude that the graph's rapid peak indicates a low energy state for nucleons within the potential well, influenced by the strong nuclear force, while the decrease in energy outside this radius is attributed to the Coulomb force. The analysis confirms that the behavior of alpha particles is closely tied to quantum mechanics principles.

PREREQUISITES
  • Quantum mechanics fundamentals
  • Understanding of alpha decay and nuclear forces
  • Familiarity with the Transmission Coefficient Equation
  • Knowledge of graph interpretation in physics
NEXT STEPS
  • Study quantum tunneling in depth
  • Explore the implications of the Transmission Coefficient in nuclear physics
  • Investigate the relationship between alpha particle energy and wavelength
  • Examine the effects of Coulomb force on particle stability
USEFUL FOR

Students and researchers in nuclear physics, particularly those studying alpha decay and quantum mechanics, will benefit from this discussion.

OhMyGod
Messages
5
Reaction score
0

Homework Statement



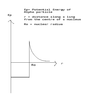
By using the graph attached,
Why high energy alpha particles are emitted by alpha-emitters of short wavelength?


Homework Equations



Transmission Coefficient Equation : T=exp(-2kd)

The Attempt at a Solution



Ain't really sure. Can't really figure out why is the graph shaped like that in the first place.
Anyone wants to give it a shot into explaining what accounts for this the shape of the graph first?



Many thanks in advance :D
 

Attachments

  • phyquest.GIF
    phyquest.GIF
    2.5 KB · Views: 545
Physics news on Phys.org
i reckon the energy of the nucleons is very low in the well, ie the nucleons are most stable there (due to conditions given by strong nuclear force), the rapid peak indicates that outside this radius, the energetic stability is very low, hence peak energy value, this subsides with increasing distance inversely with distance - arising due to coulomb force.

so am i within the 10^-15m or have i missed the point, i am humble i can handle it.
 

Similar threads

E<V Potential Step Confusion
  • · Replies 7 ·
Replies
7
Views
3K
Show that the minimum in alpha-decay spectrum is caused by interference of peak
  • · Replies 2 ·
Replies
2
Views
2K
Energy of alpha particle and quantum tunneling
  • · Replies 1 ·
Replies
1
Views
3K
Q-value and kinetic energy of alpha particle in alpha decay.
  • · Replies 2 ·
Replies
2
Views
13K
What is the Kinetic Energy of an Alpha Particle from 210Po Decay?
  • · Replies 29 ·
Replies
29
Views
8K
Estimating Half-Life of Alpha Decay: Nucleus ##^{252}_{98}Cf##
  • · Replies 2 ·
Replies
2
Views
1K
How Does Radioactive Decay Affect Current in a Spherical Capacitor Circuit?
  • · Replies 5 ·
Replies
5
Views
3K
What Are the Turning Points in Alpha Decay Potential Barrier?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Am I understanding the Geiger-Nuttall law correctly
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Will all objects in the Universe transform into black holes through quantum tunneling?
  • · Replies 7 ·
Replies
7
Views
2K