Deflection and deflection angle -Unit Load Method (Cantilever beam)

Engineering
Thread starter daphnelee-mh
Start date Nov 21, 2020
Tags

Angle Beam Cantilever beam Deflection Load Method

In summary, deflection is the amount of bending or deformation in a structural element, while deflection angle is the angle of rotation of a beam due to applied load. The Unit Load Method is a simplified technique for calculating deflection and deflection angle in cantilever beams, using unit loads at smaller sections. It differs from other methods in its simplicity and popularity among engineers. However, it is only applicable to linear elastic materials and small deflections in beams with constant cross-sectional area.

Nov 21, 2020

daphnelee-mh

Homework Statement: attached below

Relevant Equations: listed in the picture

Please help to check whether I did it correct, thanks

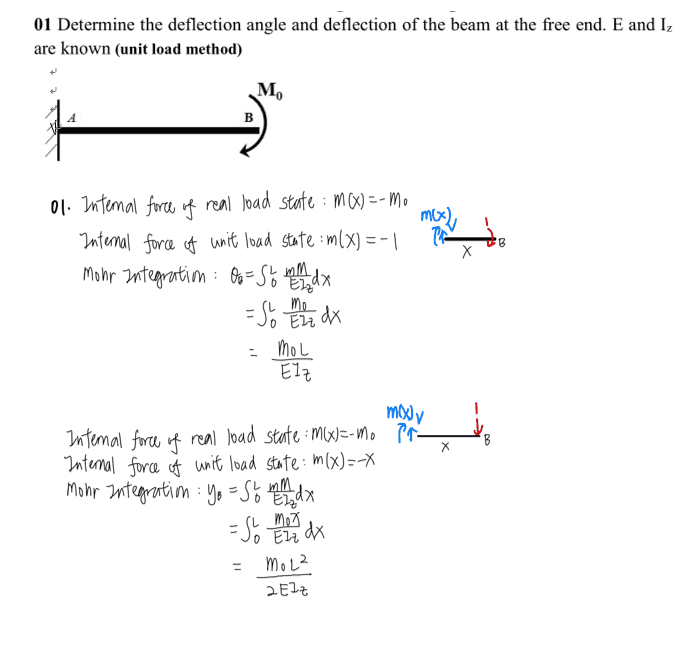
Last edited by a moderator: Nov 22, 2020

Physics news on Phys.org

Nov 21, 2020

Valkarie

It looks correct. However, it might be helpful to add a few more details to make it more complete. For example, you could provide a brief explanation of the purpose of the assignment or task, and any relevant information about the expected outcome.

1. What is deflection and deflection angle in the context of the Unit Load Method for a cantilever beam?

Deflection is the amount of bending or displacement that a beam experiences when a load is applied. The deflection angle is the angle formed between the original and deflected position of the beam. In the Unit Load Method, these values are used to calculate the maximum deflection and deflection angle of a cantilever beam under a specific load.

2. How is the Unit Load Method used to calculate deflection and deflection angle for a cantilever beam?

The Unit Load Method involves dividing the beam into smaller sections and calculating the deflection and deflection angle at each section using the formula: D = WL^3 / 3EI, where D is the deflection, W is the applied load, L is the length of the beam, E is the modulus of elasticity, and I is the moment of inertia. The total deflection and deflection angle are then determined by summing up the values for each section.

3. What are the assumptions made in the Unit Load Method for calculating deflection and deflection angle?

The Unit Load Method assumes that the beam is linearly elastic, meaning that it follows Hooke's law and has a constant modulus of elasticity. It also assumes that the beam is homogenous and isotropic, meaning that its material properties are the same in all directions. Additionally, the method assumes that the load is applied at a single point and that the beam is not subjected to any external moments.

4. How does the Unit Load Method compare to other methods for calculating deflection and deflection angle?

The Unit Load Method is a simplified approach compared to other methods, such as the Moment-Area Method or the Virtual Work Method. It is often used for quick estimations or for beams with simple load and support configurations. However, it may not provide accurate results for more complex beam designs.

5. Can the Unit Load Method be used for beams with non-uniform cross-sections?

Yes, the Unit Load Method can be used for beams with non-uniform cross-sections by dividing the beam into smaller sections with uniform cross-sections and calculating the deflection and deflection angle for each section. However, this may result in less accurate results compared to using a method specifically designed for non-uniform beams, such as the Moment-Area Method.