- #1
diemilio
- 32
- 0
Hi everyone,
I'm an electrical engineer and I'm trying to find the expression for the deflection of a clamped-clamped beam under a local distributed load. I'm not very familiar with the way the expressions for deflection are obtained, but I've seen that they can be derived in a relative straight-forward fashion. For example, I know that for a clamped-free beam with a point load at the tip, the deflection is given by: w(x) = F*L/(2E*I)*x^2*(1-X/(3L)).
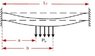
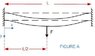
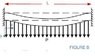
I will really appreciate if someone could please help me out with the expression for deflection as a function of distance for the case of the attached image.
Thanks in advance,
diemilio
I'm an electrical engineer and I'm trying to find the expression for the deflection of a clamped-clamped beam under a local distributed load. I'm not very familiar with the way the expressions for deflection are obtained, but I've seen that they can be derived in a relative straight-forward fashion. For example, I know that for a clamped-free beam with a point load at the tip, the deflection is given by: w(x) = F*L/(2E*I)*x^2*(1-X/(3L)).
I will really appreciate if someone could please help me out with the expression for deflection as a function of distance for the case of the attached image.
Thanks in advance,
diemilio