- #1
VyRianS
- 7
- 0
Good day all:
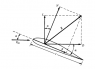
I'm having trouble deriving the forces for Lift and Drag in the attached diagram.
The text I have (Fundamentals of Aerodynamics - John Anderson) states the solution to be:
L = N cosα - A sinα
D = N sinα + A cosα
Can anyone guide me through this? I think the cofunction identity is used somewhere:
sin(90 - x) = cos x
cos(90 - x) = sin x
But that's as far as I've gotten.
Help is appreciated, thanks!
I'm having trouble deriving the forces for Lift and Drag in the attached diagram.
The text I have (Fundamentals of Aerodynamics - John Anderson) states the solution to be:
L = N cosα - A sinα
D = N sinα + A cosα
Can anyone guide me through this? I think the cofunction identity is used somewhere:
sin(90 - x) = cos x
cos(90 - x) = sin x
But that's as far as I've gotten.
Help is appreciated, thanks!