Equation of a line - Difficult problem from Thomas Calculus

[christian0710]

The problem is as follows

The perpendicular Distance ON from the origin to line L is p, and ON makes an angle α with the positive x-axis. Show that L has the equation x*cosα + y*sinα = p

What I've done
First I made a drawing from the text and I assume ON and P are the same thing.

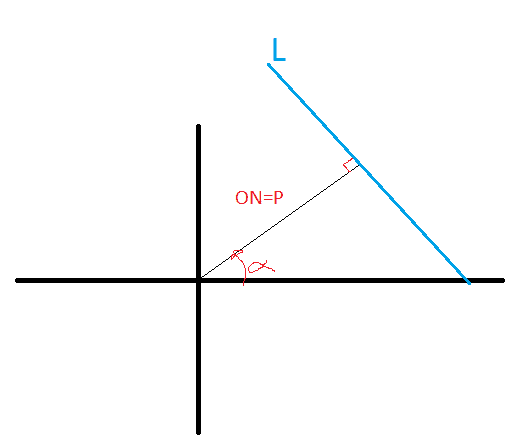
Then I thought "How do I derive the equation for a line from this information?" I could try the equation of a line (y2-y1)=m(x2-x1) and if i know that the slope of the line ON is tan(α), thn the slope of the perpendicular line must be tan(α+90). But from thereon I'm somewhat stuck.

 

[PFuser1232]

Hint: if lines $L_1$ and $L_2$ are perpendicular, then $m_1 m_2 = -1$.
Also, think about the point of intersection between the line and $OP$. Can you find the coordinates of the point of intersection in terms of $\alpha$?
Next time use the template.

 

[christian0710]

Hint: if lines $L_1$ and $L_2$ are perpendicular, then $m_1 m_2 = -1$.
.

So if m1*m2 = -1 then the slope of of line L must be m2=-1/m1 =-1/tan(alpha) Right?

Also, think about the point of intersection between the line and $OP$. Can you find the coordinates of the point of intersection in terms of $\alpha$?
Next time use the template.

I know that if the slope of a line is known and we multiply the slope with the run/horizontal length then we get the rise/y-cordinate/height.
So i guess we can find the y-intercept as m=Δy/Δx --> mΔx=Δy, --> and we can find the adjacent side of the right triangle Δx and the opposite side Δy If we assume the line is one unit of length, because then we know that cos(α)=adjacent/hyp = adjacent/1 so actually cos(α)=x and sin(α)=y

But here I'm stuck. Is this correct so far?

 

[HallsofIvy]

You have a right triangle in which one angle has measure $\alpha$, the leg at that angle has length p, and the hypotenuse is the x axis- from the origin to the x-intercept of the line: [itex]cos(\alpha)= p/x[itex]. Find the x-coordinate of the x-intercept.

 

[christian0710]

You have a right triangle in which one angle has measure $\alpha$, the leg at that angle has length p, and the hypotenuse is the x axis- from the origin to the x-intercept of the line: [itex]cos(\alpha)= p/x[itex]. Find the x-coordinate of the x-intercept.

Hi thank you for the reply. So if the hypothenus is the x-axis, then my drawing must be wrong or i would have to rotate it clockwise so the hypotenus lies along the x-axis?
But I'm confused now beause in the text it says "ON(same as P) makes an angle alpha with the positive x-axis, so according to the text it sounds to me like the line ON(the hypotenus) does not lie on the x-axis but rather makes an angle with it?

 

[hunt_mat]

You know the length of ON=p, and you know the gradient of the line. From this you should be able to compute the point of intersection. You know the gradient of L. You have everything to need.

 

[PFuser1232]

So if m1*m2 = -1 thenpe of of line L must be m2=-1/m1 =-1/tan(alpha) Right?
I know that if the slope of a line is known and we multiply the slope with the run/horizontal length then we get the rise/y-cordinate/height.
So i guess we can find the y-intercept as m=Δy/Δx --> mΔx=Δy, --> and we can find the adjacent side of the right triangle Δx and the opposite side Δy If we assume the line is one unit of length, because then we know that cos(α)=adjacent/hyp = adjacent/1 so actually cos(α)=x and sin(α)=y

But here I'm stuck. Is this correct so far?

Yes. The slope of the line is $-\frac{1}{\tan{\alpha}}$, and the coordinates of the point of intersection are $(\cos{\alpha},\sin{\alpha})$.
Now, given the fact that $(\cos{\alpha},\sin{\alpha})$ is on line $L$, and that the gradient of $L$ is $-\frac{1}{\tan{\alpha}}$, can you find the equation of the line?

 

[NascentOxygen]

So if the hypothenus is the x-axis, then my drawing must be wrong or i would have to rotate it clockwise so the hypotenus lies along the x-axis?

You have marked a right angle in your drawing, and now need to mark in its neighbouring right angle. Then you'll see your right-anged triangle with its hypotenuse lying on the x axis.

The hypotenuse is the side opposite to the right angle in a right-angled triangle.

 

[LCKurtz]

If you still don't have it figured out maybe this approach would help you. Call the origin $O$, the perpendicular intersection point $P$ and and a variable point $(x,y)$ on the line $Q$. Figure out the coordinates of $P$ from the picture. Then the dot product $\vec{OP}\cdot \vec{PQ}=0$ since they are perpendicular. What does that give you?