Derivation of stiffness matrix for a beam and other related questions

[Sadeq]

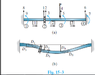
My main question is why we derive the structure matrix for a beam like the attached first picture; we assume the beam on the left on point B has no deflection? While i check this by computer analsysis program and it has an effect. Please explain in details

The second question is the displacement at nodal 2 has two vertical displacements and one rotation??
Why?? The logic says 1 vertical and no displacement since there is moment to prevent rotation
See picture 3 and 4 which are symbol and illustration


My third question why in truss the axial stiffness is much larger than shear and flexural stiffness, they always depend on the dimension and modules of elasticity so why in truss its larger and in beam it very small, why?
I appreciate your help, please explain in details

 

[PhanthomJay]

Regarding the first figure, it is misleading. It assumes that the beam is fixed at support B (no rotation or translation) probably as a first step in your analysis in determining stiffnesses (as in ''moment distribution'' method). Ultimately, however, that joint is released so that the member does rotate about B just like it does at C, and the deflected shape takes on a different pattern.

I don't understand the next set of figures.

Question 3: A pure truss consists of triangularly connected members with loads applied at the joints only, with no loads in between. As such, all members are 2-force members that take axial loads (tension or compression) only, no flexure or shears in members. In beams, often the flexural and shear stresses are large compared to the axial stress, when the prime source of loading is vertically applied between joints.

 

[Sadeq]

Thank you very much.
for the first question, the reason of this is that we use fixed fixed assumption(that what i understand)

the second, the arrows one and two represent vertical dispacement while 3 represent roration( all free degree of freedom)
so i was confused why there any two vertical dispalcment and why rotation is allowed

the third, so i can understand what you said, and this implies this not related to the value of EA/L or 12EI/L^3, because they will be always the same for the section , it just related to the way of loading the member, which ceate forces.Right

Thank you another time. you help me a lot
hope i can someday return your favor

 

[PhanthomJay]

Oh in question 2 the node at 2 is a slider or guided connection. In a guided connection, the beam can translate at that node, but there isn't relative rotation between beams, they must both remain 90 degrees to the slider as the joint rotates. Those forces 1 and 2 I gather are the shear forces at each end of the beams.
I am not sure of your question 3 ; in a truss, loads are axial along the members, and the members are subject to tension or compression stresses, and axial deformations only, with the stiffness of a member equal to AE/L if you need to know that.

 

[PhanthomJay]

Just thinking there may be sum confusion between a slider joint and a slider support . You have a joint that connects the 2 beams. The joint can translate and rotate, and in doing so, the beams remain at 90 degrees to the slider. If it was a slider support, the support could translate but not rotate, and the beams still stay at 90 degrees to it.

 

[Sadeq]

Thank you man