Derivation of the error due to a finite load attached to a potentiometer

[Weaver]

Homework Statement

Derivation of error due to finite load attached to potentiometer

Relevant Equations

(Included in main body, so that it formats correctly)

x = fraction of potentiometer connected to load
V_p in parrallel with V_L = x/(R_p/R_L.x.(1-x) + 1)

If R_L = infinite, then R_o = x and V_o = x.Vs
If R_L = finite, then R_o = x/(R_p/R_L.x.(1-x) + 1) and V_o = x.V_s/(R_p/R_L.x.(1-x) + 1)

Therefore error is x.V_s - x.V_s/(R_p/R_L.x.(1-x) + 1)

Trying to break the equation down further, I did the following :

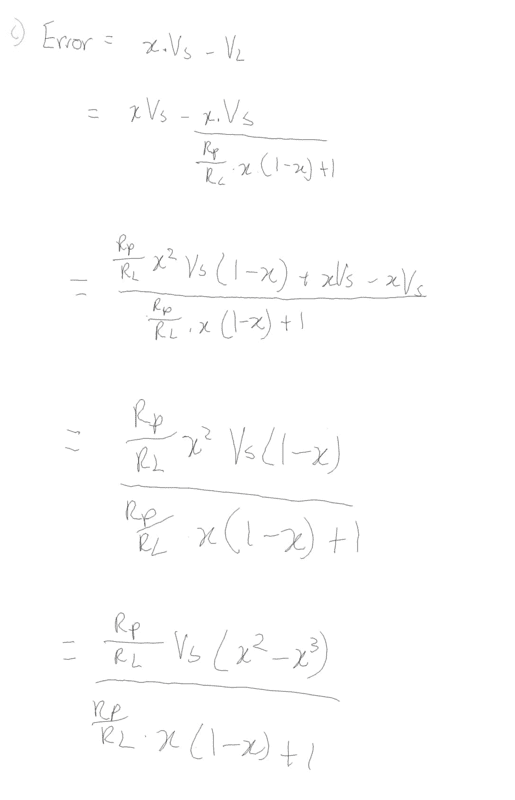
However, the final equation, is supposed to be (R_p/R_L).V_s.(x²-x³)

Do you just ignore the denominator, or am I missing a step?

I appreciate any help or advice

 

[berkeman]

Sorry, I'm not able to decode your equations at all. Others may be able to, though.

It always helps to start with a schematic or figure, to be sure everybody understands the terminology and the variables. For example, I have no idea what you mean by:

Vp in parrallel with VL

And I'm not able to understand your use of parenthesis. I think that I finally figured out that "." means multiplication, but I'm not even sure about that.

In general, it's best if you learn to use basic LaTeX for writing math equations online. We have a tutorial on that under INFO, Help at the top of the page.

In any case, I would think the error would be the difference in the wiper voltage between having the load resistor connected or not, right?

https://upload.wikimedia.org/wikipe...oad.svg/474px-Potentiometer_with_load.svg.png

If RL is infinite, then you just get the voltage divider between R1 and R2. If RL is finite, that modifies the voltage divider equation. Is that what you were trying to do with your work?

 

[Weaver]

Sorry, I'm not able to decode your equations at all. Others may be able to, though.

It always helps to start with a schematic or figure, to be sure everybody understands the terminology and the variables. For example, I have no idea what you mean by:

And I'm not able to understand your use of parenthesis. I think that I finally figured out that "." means multiplication, but I'm not even sure about that.

In general, it's best if you learn to use basic LaTeX for writing math equations online. We have a tutorial on that under INFO, Help at the top of the page.

In any case, I would think the error would be the difference in the wiper voltage between having the load resistor connected or not, right?

https://upload.wikimedia.org/wikipe...oad.svg/474px-Potentiometer_with_load.svg.png

View attachment 260259

If RL is infinite, then you just get the voltage divider between R1 and R2. If RL is finite, that modifies the voltage divider equation. Is that what you were trying to do with your work?

Hi, thanks for your reply! I didn't know LaTeX was an option for writing equations on here. I've re-done them below. I thought "." was a common convention for multiply, but maybe that's just in Europe. Sorry about the confusion. I've used "*" this time around for the multiply symbol.

The diagram you attached is correct and I think we are on the same page. Essentially, I am looking to calculate the error from having R_L as infinite and finite.

In the case of my workings, $$R_1 = (1-x)*R_p\ and\ R_2 = x*R_p$$

where x is the fraction of the resitor the wiper is at.

From this:

$$V_{out} =\frac{V_s}{R_{total}} * R_{out}$$

$$R_{out} = x * R_p || R_L$$
$$R_{out} = \frac{x*R_p*R_L}{x*R_p + R_L}$$

$$R_{total} = (1-x)*R_p + R_{out}$$
$$R_{total} = (1-x)*R_p + \frac{x*R_p*R_L}{x*R_p + R_L}$$

=> $$V_{out} = \frac{V_s}{(1-x)*R_p + \frac{x*R_p*R_L}{x*R_p + R_L}} * \frac{x*R_p*R_L}{x*R_p + R_L}$$
$$V_{out} = \frac{V_s*x}{\frac{R_p}{R_L}*(1-x) + 1}$$

With an infinite R_L, $$\frac{R_p}{R_L} = 0$$ => $$V_{out} = V_s * x$$

With a finite R _L, it can't be simplified

Following from this, the error is then
$$x*Vs - \frac{V_s*x}{\frac{R_p}{R_L}*(1-x) + 1}$$

Which I then break down in my workings from the previous post to :
$$\frac{ \frac{R_p}{R_L} * V_s * (x^2-x^3)}{\frac{R_p}{R_L}*(1-x) + 1}$$

However, in my lecture slides and textbooks, the correct result for error is:

$$\frac{Rp}{RL} * V_s * (x^2-x^3)$$

I don't see the step in between my final line of workings and that? I assume I am missing something else? Thanks

 

[berkeman]

Thanks! The LaTeX makes it so much easier to read and quote...

=> $$V_{out} = \frac{V_s}{(1-x)*R_p + \frac{x*R_p*R_L}{x*R_p + R_L}} * \frac{x*R_p*R_L}{x*R_p + R_L}$$
$$V_{out} = \frac{V_s*x}{\frac{R_p}{R_L}*(1-x) + 1}$$

I get an extra x term in the denominator here:

$$V_{out} = \frac{V_s*x}{\frac{x*R_p}{R_L}*(1-x) + 1}$$

I still need to check it again, but can you go through this set of steps one more time to see if you get that extra "x" also?

 

[Weaver]

I get an extra x term in the denominator here:
$$V_{out} = \frac{V_s*x}{\frac{x*R_p}{R_L}*(1-x) + 1}$$

I still need to check it again, but can you go through this set of steps one more time to see if you get that extra "x" also?

Thanks. Yeah, there should be another x there. Nice spot! Made that mistake when typing. I then copied and pasted so it carries throughout the rest My written workings in the original post however has that x so it doesn't solve my problem. My typed workings though, from there on should be:

---------------------------------------------------------------------------------------------------------------------------------------------------------
$$V_{out} =\frac{V_s}{R_{total}} * R_{out}$$
=> $$V_{out} = \frac{V_s}{(1-x)*R_p + \frac{x*R_p*R_L}{x*R_p + R_L}} * \frac{x*R_p*R_L}{x*R_p + R_L}$$
$$V_{out} = \frac{V_s*x}{\frac{R_p}{R_L}*x*(1-x) + 1}$$

With an infinite R_L, $$\frac{R_p}{R_L} = 0$$ => $$V_{out} = V_s * x$$

With a finite R _L, it can't be simplified

Following from this, the error is then
$$x*Vs - \frac{V_s*x}{\frac{R_p}{R_L}*x*(1-x) + 1}$$

Which I then break down in my workings from the previous post to :
$$\frac{ \frac{R_p}{R_L} * V_s * (x^2-x^3)}{\frac{R_p}{R_L}*x*(1-x) + 1}$$

However, in my lecture slides and textbooks, the correct result for error is:

$$\frac{R_p}{R_L} * V_s * (x^2-x^3)$$
--------------------------------------------------------------------------------------------------------------------------------------------------------

Thanks

 

[berkeman]

Following from this, the error is then
$$x*Vs - \frac{V_s*x}{\frac{R_p}{R_L}*x*(1-x) + 1}$$

Which I then break down in my workings from the previous post to :
$$\frac{ \frac{R_p}{R_L} * V_s * (x^2-x^3)}{\frac{R_p}{R_L}*x*(1-x) + 1}$$

However, in my lecture slides and textbooks, the correct result for error is:

$$\frac{R_p}{R_L} * V_s * (x^2-x^3)$$
--------------------------------------------------------------------------------------------------------------------------------------------------------

Thanks

Did they specify at some point how to define the error? You start to derive it with a subtraction above, but I would have thought that the error was mainly the denominator that modifies x * Vs.

Anyway, maybe try substituting some real values into each equation to see if you get the right answer with your subtraction equation versus the final result in the book. I would use Vs = 10, Rp = 10, RL = 5, and x = 0.5. That makes a pretty easy voltage divider equation, so you should be able to test the results that you are getting to see if they give the right answer.