Potentiometer position problem

[StokeBoy]

Homework Statement

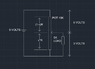
The problem that is that of a loaded potentiometer and the position on the slider. The question is that a 10k Ohm potentiometer is connected across a 9 volt dc supply. Across the bottom part of the POT a 5k Ohm resistive load is connected which has 3 volts developed across it. Decide the position of the slider on the potentiometer to get 3 Volts across the load.

Homework Equations

VL = Vs*(R1/R1+R2) Where R1 it the top of the POT and R2 is the Bottom of the POT with the load across it

The Attempt at a Solution

I have got this far and tried many attempts at solving for x. I understand that it will be a proportion or ratio of the POT resistance.

[(x*Rp)*RL/(x*Rp)+RL]
VL=Vs* _________________________ Where VL = Voltage Load
[(x*Rp)*RL/(x*Rp)+RL]+(1-x)RL Vs = Voltage Supply
Rp = Res Potentiometer
RL = Res Load

I would much appreciate it if somebody knows if I'm taking the right approach and if so how on Earth do I solve for x. Just basic steps would be helpful. Every time I try to do it I just end up in a complete mess. It's driving me crazy.
https://physicsforums-bernhardtmediall.netdna-ssl.com/data/attachments/60/60520-9dbe04eb6c8910a17f39930ad611a216.jpg

 

[mfb]

VL = Vs*(R1/R1+R2)

There are brackets missing, and there is another error in the equation. Where is the load, where is R1?

[(x*Rp)*RL/(x*Rp)+RL]

Where does that expression come from and what does it mean?

Every time I try to do it I just end up in a complete mess.

It would help to see those steps (and an explanation what you are doing) instead of just the final mess.

 

[StokeBoy]

Sorry I messed up the original message by trying to make it more readable. The equation should read:

VL=Vs*[(x*Rp)*RL/(x*Rp)+RL]/[(x*Rp)*RL/(x*Rp)+RL]+(1-x)RL Vs]

I've tried to portion the POTENTIOMETER into x*Rp and (1-x)Rp and fitted it into the voltage divider formula VL=Vs*R1/R1+R2. I thought that was the way to go with the question.

 

[mfb]

Vs*R1/(R1+R2) will indeed give "a" voltage in the circuit if you calculate R2 correctly, but not the load voltage.

 

[gneill]

A useful property of voltage dividers is that they're all about ratios: The ratio the input to the output voltage; the ratio of resistances. As such they are amenable to scaling the values involved to make the math a bit cleaner (not necessarily simpler, but easier to manipulate).

For example, in this problem the input voltage is 9 V and the output 3 V. Well that's just a 3 to 1 ratio. So the potentiometer position will exactly the same if we set the input to 3 and expect 1 at the output. Do the same for the given resistor values to reduce them to simple numbers (they will be small integers in this case). Since you're looking for the POT position, once you find a value for either the "top" or "bottom" portion of the total POT value you automatically know the other portion's value.

 

[mfb]

@gneill: Well, you still have to work with a variable for a while because one side has another resistor in parallel. The small numbers appear in the result afterwards.

 

[gneill]

@gneill: Well, you still have to work with a variable for a while because one side has another resistor in parallel. The small numbers appear in the result afterwards.

Yup. One variable. But that load "resistor" now has a unitless value of 1. That simplifies the expression for the parallel combination with the bottom of the POT. It makes getting to the final quadratic equation less math-tedious.