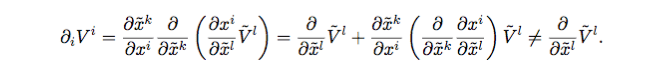I Uncovering the Derivative of a Tensor: Understanding its Equations and Origins

[mk9898]

How/why does the first equal sign hold? Where does each derivative come from:

 

[Orodruin]

Its just the chain rule and the transformation properties of the vector components.

 

[mk9898]

Ahh they just switched the two chain rule derivatives. Got it. Thank you. Another question: is the second equal sign correct? Why does the first term only have one derivative?

 

[Orodruin]

The second equal sign is correct. Apply the product rule. The first term arises from the derivative acting on the vector component and the derivatives outside cancelling (another instance of the chain rule).

 

[mk9898]

I'm not seeing how they cancel since they are operators.

Here is what I see:

$\frac{\partial \tilde x^k}{\partial x^i}\frac{\partial^2 x^i}{\partial \tilde x^k \partial \tilde x^l}$But since they are operators, I don't see how the two can cancel each other out and the fact it's the derivative squared so we cannot move one of derivatives to the right and let them somehow cancel out like so:

$\frac{\partial \tilde x^k}{\partial x^i}\frac{\partial x^i \partial}{\partial \tilde x^k \partial \tilde x^l}$

Is it due to the uniqueness of the dependence of the vector components that they are the inverse of one another?

 

[Orodruin]

I'm not seeing how they cancel since they are operators.

That is the second term, not the first term...

 

[mk9898]

Ah got it. Yea it's just then the Kronecker delta and the k's become l's. Got it thanks!