amanda.ka
- 46
- 0
Homework Statement
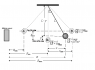
I did an experiment to test the conservation of mechanical energy in an oscillating pendulum. As part of the analysis I had to find the pendulum's vertical position with time using the formula: y = L-sqrt(L^2-x^2) where L was the pendulum's length (L=1 m). Then for the next step I had to find the vertical velocity vs. time. The instructions say that it can be found using derivative(y) so my question is how do I take the derivative of L-sqrt(L^2-x^2)?
Homework Equations
The Attempt at a Solution
When I tried to derive it I got:
f(x) = L - sqrt(L^2 - x^2) = L - (L^2 - x^2)^(1/2)
{d/dx}[f(x)] = f'(x) = - (1/2)[(L^2 - x^2)^(-1/2)][- 2x]
= x(L^2 - x^2)^(-1/2).
I think I did something wrong because when I put in the values of "x" I do not get the same answers as the computer program I am using to generate the graphs did. I have to show a sample calculation of how the data for the graph was calculated so any help would be appreciated, thanks!