Sorry, there was no math to be done, when I wrote the parametrization I should have written ##x=a \cosh \theta## and ##y=a\sinh \theta##.
The fundamental points in all this are:
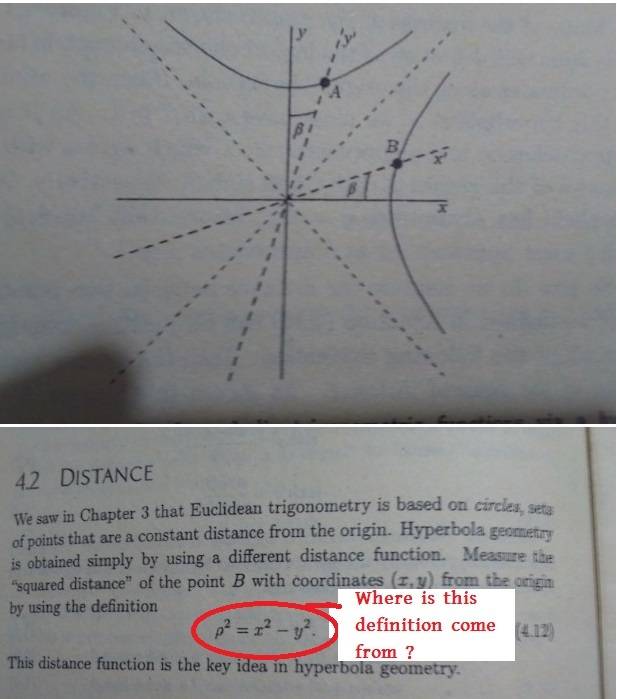
What do we call distance?
In Euclidean geometry, we say that two points that belong to the same circle (centred at the origin) are at the same distance (from the origin). The equation for a circle is simply ##x^2+y^2=\text{ct.}## (here and elsewhere in my post ##\text{ct.}## means "constant" nothing to do with time and speed of light) then we can define the distance as this constant, so for example, any point that belongs to the circle ##x^2+y^2=2## will be at a distance 2.
In Hyperbolic geometry, we say that two points are at the same distance is they belong to the same hyperbola, the mathematical equation for a hyperbola is just ##x^2-y^2 = \text{ct.}##, and as in EG we define this constant to be de distance.
What is your definition of a hyperbola?
Of course all this depends on ##x^2-y^2=\text{ct.}## being your definition of hyperbola, so for us to help you further we need to know what is your precise definition of a hyperbola, whatever it is, there is a way to prove that is equivalent to ##x^2-y^2=\text{ct.}##