Derive that the lagrangian in classical phyics is L=T-V

[Gavroy]

Hey,

can somebody show me how to derive that the lagrangian in classical phyics is L=T-V

i have seen this formula so many times, but i have no idea where it really comes from?

 

[arildno]

Two levels of answer:
1. That particular choice of integrand will, by the calculus of variations yield the correct equations of motion. That is, the formula works

2. An independent, deep reason for the physical importance of the formula:
I dunno.

 

[K^2]

Well, if you happen to have a Hamiltonian handy, it's easy to derive the Lagrangian from it.

L = \dot{q}p - H

Where q is generalized coordinate and p is generalized momentum. Again, if you aren't certain what generalized momentum is that corresponds to your generalized coordinate, there is a way to obtain it from Hamiltonian.

\dot{p} = -\frac{\partial H}{\partial q}

At any rate, in classical mechanics, you can usually express the relationship between p and q differently.

p = M\dot{q}

Where M is a generalization of mass. For example, if you are talking about rotation, where p is angular momentum and q is angle, M will become moment of inertia.

Wit this in mind, we can rewrite an earlier expression.

\dot{q}p = M \dot{q}^2 = 2T

Again, think about rotation, T = ½Iω².

And so the equation for Lagrangian becomes this.

L = \dot{q}p - H = 2T - (T + U) = T - U

Just keep in mind that this is specific to Classical Mechanics. Once you go Relativistic or Quantum, you have to be more careful.

 

[Gavroy]

okay thank you, but for this reasoning it is necessary to know the expression for momentum in classical mechanics, isn't it possible to derive the formula without referring to other formulas that are not part of the variational principle.

 

[K^2]

If you take principle of extreme action as an axiom, sure. This is more of where the principle of extreme action comes from if you start from Hamiltonian.

\frac{\partial L}{\partial q} - \frac{d}{dt} \frac{\partial L}{\partial \dot{q}} = \frac{d}{dt} \frac{\partial H}{\partial \dot{q}} - \frac{\partial H}{\partial q} - \dot{p} = \dot{p} - \dot{p} = 0

So Euler-Lagrange equation can be derived using Hamiltonian Mechanics, and since Euler-Lagrange equation guarantees extreme action, principle of extreme action can be seen as its consequence.

 

[Cleonis]

Hey,
can somebody show me how to derive that the lagrangian in classical phyics is L=T-V

i have seen this formula so many times, but i have no idea where it really comes from?

Well, in classical mechanics the principle of least action and the work-energy theorem are mathematically equivalent. The challenge is to show that in a clear and straightforward manner.

I'm currently preparing a discussion of L=T-V for my own website. The planned animations are ready - I should be able to finish up tomorrow or so, so stay tuned.

The outline is as follows:
As we know: a true worldline has the following property: at every point along the wordline the change of kinetic energy and the change of potential energy match each other.

Try a range of worldlines. For each worldline, plot separately a graph for the kinetic energy at each point in time and for the potential energy at each point in time.

Next, examine how the graphs change as a function of varying the worldline. I will refer to the shapes of the graphs as 'profiles'.
Kinetic energy is proportional to the square of velocity, hence the profile of the kinetic energy relates quadratically to deviation from the true worldline. The profile of the potential energy changes linearly with deviation from the true worldline.

Here's the rub: take a graph of a parabola, and subtract a graph of a straight line from that: the result is another parabola.
That is what the principle of least action does: you integrate the kinetic energy, and you integrate the potential energy, condensing the profile to a number. You can graph that as a function of deviation from the true worldline. The subtraction gives a parabola that is at its minimum at the true worldline.

What I just wrote is the general outline; the article on my website will be illustrated with animations.

Cleonis
http://www.cleonis.nl

 

[K^2]

There are infinitely many worldlines that satisfy T+U = constant, yet do not satisfy extreme action, and therefore, are non possible. So there is a flaw in your argument somewhere.

 

[Cleonis]

isn't it possible to derive the formula without referring to other formulas that are not part of the variational principle.

No, that isn't possible.

The variational approach is a mathematical tool that does not in itself single out a particular form. The only way to arrive at L = T-V is to start out with something equivalent.

That is what the derivations for classical mechanics do: you put in F=ma, or the work-energy theorem, and that narrows things down to L=T-V

 

[Cleonis]

in classical mechanics the principle of least action and the work-energy theorem are mathematically equivalent.

I have uploaded the discussion of L=T-V to my website. The title of the page is http://www.cleonis.nl/physics/phys256/least_action.php"

I'll broaden the mathematical discussion in the coming weeks.
I used a Java applet to doublecheck the integrations and so on. I will make that applet available. The applet was also used to generate the animations. The applet adds interactivity; you can move around a slider to vary the worldline.

 

[Cleonis]

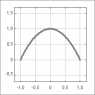
I will discuss the following case: an object shoots upward, released to free motion. The object climbs for a second, decelerated by gravity, and falls back again.

To work with round numbers I have selected the following conditions:
- Total duration: 2 seconds (from t=-1 to t=1)
- Gravitational acceleration: 2 m/s²
- Mass of the object: 1 unit of mass.

Those conditions imply that along the true worldline the starting velocity is
2 m/s, and the object climbs to a height of 1 meter. The parabola is given by the function:

f(t) = -(t + 1)(t - 1) = -t^2 +1

The worldline is varied, generating a class of trial worldlines. The startpoint and endpoint (at t=-1 and t=1) are fixed, in between the wordline is varied.
I introduce a factor p_v which stands for 'variational parameter'. This gives me a function of two variables: 't' and 'p_v'.

f(t,p_v) = -(1 + p_v)(-t^2 + 1)

The time derivative to get the velocity:

v(t,p_v) = -2(1 + p_v)t

I will follow the convention of denoting kinetic energy with T and potential energy with V.

The kinetic energy and the potential energy:
(as I said, for simplicity I use 2 units of acceleration.)

T(t,p_v) = 2(1 + p_v)^2t^2

V(t,p_v) = 2(1 + p_v)(-t^2 + 1)

This is where the work-energy theorem enters. At every point along the worldline the change in kinetic energy matches the amount of work done.

The next step is to obtain expressions for time integrals of the kinetic energy and the potential energy respectively. The integrals are from t=-1 to t=1.

\int\limits_{-1}^{1} T(t,p_v) \, dt = \frac{4}{3}(1+p_v)^2

\int\limits_{-1}^{1} V(t,p_v) \, dt = \frac{8}{3}(1+p_v)

I will use the notation S_T for the 'Kinetic energy component of the action', and S_V for the 'Potential energy component of the action'.

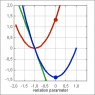
In the diagram the red line is the graph of S_T as a function of p_v The green line graphs the negative of S_V The blue line graphs the action.

The action, the blue parabola, is the red parabola combined with the green line. In a graph, when you add a line to a parabola you get another parabola, but with the minimum shifted sideways.


The minimum of the action

The shifted minimum is at the point where the upward slope of the red parabola matches the downward slope of the line. Hence the derivative of S_V must be subtracted from the derivative of S_T

\cfrac{dS_T}{dp_v} - \cfrac{dS_V}{dp_v} = 0

\frac{8}{3}(1+p_v) - \frac{8}{3} = 0

This confirms that the action is least when p_v is zero.


Cleonis
http://www.cleonis.nl

 

[K^2]

And? You proved for this particular problem with this particular variation, the minimum is achieved with the trajectory you provide. Why is that trajectory the real trajectory? Where do you prove that no other form of variation could reduce the action? What is the point of this special case when it says absolutely nothing about the general case?

 

[facenian]

okay thank you, but for this reasoning it is necessary to know the expression for momentum in classical mechanics, isn't it possible to derive the formula without referring to other formulas that are not part of the variational principle.

I think it is possibe. You have to use Newton's 2nd law and the principle that states that the work done by virtual displacements is null and you can derive lagrange equations when the constraints are holomorphic and the forces (other than constraints forces) come from a potencial.

 

[Cleonis]

And? You proved for this particular problem with this particular variation, the minimum is achieved with the trajectory you provide. Why is that trajectory the real trajectory? Where do you prove that no other form of variation could reduce the action? What is the point of this special case when it says absolutely nothing about the general case?

The question of the original poster was where the Lagrangian, (T-V), comes from. Well, the Lagrangian comes from a geometrical property of parabola's; if you add a straight line to a parabola you get a copy of the original parabola, but shifted sideways.


The kinetic energy relates quadratically to variation of the worldline, for the potential energy the relation is linear. This quadratic-linear difference is key; it applies for any trajectory and any variation of it.
The principle of least action arises from the quadratic-linear difference.

Proofs that the principle of least action implies the work-energy theorem already exist, but these proofs are in the form of abstract mathematics. My goal is to provide insight into where the Lagrangian comes from.


Generalizing the demo

It would be interesting, of course, to generalize the demonstration. For one thing, It doesn't just work for an acceleration of 2; it works for any acceleration.

When acceleration is uniform then distance traveled relates quadratically to time, which means a graph of the trajectory is a parabola. But it would be interesting to show that the principle of least action holds good for any part of that parabola.

 

[K^2]

You're not making any sense. First of all, I can come up with a variation on a world line that will give kinetic energy variation that's linear in variation parameter.

And in either case, your argument doesn't make any sense. You insist that variation of T-U is quadratic in parameter. Suppose I give you this one. What of it?

 

[Cleonis]

I can come up with a variation on a world line that will give kinetic energy variation that's linear in variation parameter.

Well, to calculate the kinetic energy you square the velocity. Kinetic energy is inherently quadratic.

I wonder what variation you have in mind.
I suppose one can opt to make the variation paramater p_v a function of yet another parameter. I will call the second parameter p_yap (yap = Yet Another Parameter)
One can opt to define p_v = sqrt(p_yap)

Perhaps it's possible to come up with a scheme in which the kinetic energy is a linear function of p_yap, I don't know.
Anyway, such a parameterization will not alter the physics content of the case. For instance, there is no scheme in which kinetic energy and potential energy are simultaneously a linear function of the parameterization.

Independent of the parameterization, the differences between kinetic energy and potential energy are a given.

 

[K^2]

2-dimensional motion in polar coordinates. In order to get correct EQMs, Lagrangian must include centrifugal term. Now both kinetic and potential energies have ω² term in them. So I can easily make a linear deviation in both Kinetic and Potential energy using the same trick.

And it still doesn't matter. You are still not explaining how any of this results in your claim that this has anything to do with where Lagrangian comes from.

 

[Cleonis]

In post #10 I used an acceleration of 2 units. Here is the counterpart with the acceleration represented with symbol 'a', to generalize to all values of 'a'. The duration is set from t=-1 to t=1

The position as a function of time is given by (h is the height that the object reaches):

f(t) = -\frac{1}{2}at^2 + h

Given the duration the height follows from the acceleration: h=1/2a

f(t) = \frac{1}{2}a(- t^2 + 1)

The worldline is varied, generating a class of trial worldlines.

f(t,p_v) = (1 + p_v)(\frac{1}{2}a(-t^2 + 1))

The time derivative to get the velocity:

v(t,p_v) = -(1 + p_v)at

The kinetic energy and the potential energy:

T(t,p_v) = \frac{1}{2}(1 + p_v)^2a^2t^2

V(t,p_v) = a(1 + p_v)(\frac{1}{2}a(-t^2 + 1))

The time integrals of the kinetic energy and the potential energy respectively.

\int\limits_{-1}^{1} T(t,p_v) \, dt = \frac{1}{3}a^2(1 + p_v)^2

\int\limits_{-1}^{1} V(t,p_v) \, dt = \frac{2}{3}a^2(1 + p_v)

I will use the notation S_T for the 'Kinetic energy component of the action', and S_V for the 'Potential energy component of the action'.

The minimum of the action

The shifted minimum is at the point where the upward slope of the red parabola matches the downward slope of the line. In other words, when the derivative of S_V subtracted from the derivative of S_T equals zero the action is at its minimum.

\cfrac{dS_T}{dp_v} - \cfrac{dS_V}{dp_v} = 0

\frac{2}{3}a^2(1+p_v) - \frac{2}{3}a^2 = 0

Hence when p_v is zero the action is at its minimum.Cleonis
http://www.cleonis.nl

 

[cosmicraj]

Well, in classical mechanics the principle of least action and the work-energy theorem are mathematically equivalent.

Actually I do not think you can say this beacuse those are not equivalent. Energy Conservation is due to the time invarients. That is some quantity will not change as times goes on.
Energy Conservation is Hamiltonian.

If you need i can show you that result.
Finally you get from Principle of Least Action and Time Symmetry
L-(dq/dt)Pi as a conserved Quantity
where Pi is the canonically Conjugate momentum with respect to q

If you need i will give you the result.

 

[miguelbbr]

Elastic potential energy usually have quadratic form.

 

[sentinel]

A good source:Classical dynamics of particles and systems (Marrion, Jerry B)

 

[2VtQCxn]

OP: I think you were looking for something more fundamental.

The form of the Lagrangian follows from constraints we assume the laws of physics must obey in classical mechanics.

First, assume that there exists a frame of reference in which space and time are homogeneous and isotropic; this is called an inertial frame. Consider the simplest nontrivial mechanical system: a free particle. Since the laws of physics will be expressed in the Lagrangian, the only quantity it can depend on (barring any terms of the form df(q,t)/dt, which don't affect the equations of motion) is the magnitude of the particle's velocity. It will be convenient to write this Lagrangian as L(v^2).

Next, assume Galileo's relativity principle: any frame given by adding a constant velocity to an inertial frame is inertial. In particular, an infinitesimal change in the velocity of a free particle should yield an equivalent Lagrangian; that is, the difference must be of the form df(q,t)/dt. To first order, we have

L((v+\epsilon)^2) = L(v^2) + \frac{\partial L}{\partial v^2} 2 v \cdot \epsilon

For the two Lagrangians to be equivalent, the second term on the right must be linear in v, so L is proportional to v^2. We call the proportionality constant m/2. You will recognize now that L for a free particle is simply what we call the kinetic energy.

To describe a closed system of particles, we may account for their interactions by adding a term -U(q1,...,qn). We then recover Newton's second law by defining force as the negative gradient of U. To why only this and not something else, I guess the answer is "just because". Why F=ma, after all?

Check out the first chapter of the first volume of Landau and Lifgarbagez for more.

 

[lalbatros]

Well, for particle moving in an electromagnetic field, we have:

L = T - V + q/c A.v

The rule L = T-V is not a general rule.
The special case "T-V" occurs only when the Hamiltonian is the sum of a momentum term and a coordinate term.
(my guess, to be checked)

 

[2VtQCxn]

Well, for particle moving in an electromagnetic field, we have:

L = T - V + q/c A.v

And indeed that is what led Einstein to relativistic mechanics, as noted here:
http://en.wikipedia.org/wiki/Galilean_relativity#Electromagnetism

 

[dextercioby]

For non-relativistic mechanics, an argument would be to choose the lagrangian action equal to

S_{L}[x,\dot{x}]=\int_{t_{1}}^{t_{2}} L(x,\dot{x},t) \, dt

subject to specific limit conditions and derive the Euler-Lagrange equations

\frac{\partial L}{\partial x} - \frac{d}{dt} \frac{\partial L}{\partial \dot{x}} = 0

For a Newtonian system in a potential field, Newton's equations read

m\frac{d\dot{x}}{dt} = -\frac{\partial V(x,t)}{\partial x}

Comparing the 2 OD equations one finds a simple formula for L

L=m\frac{\dot{x}^2}{2} - V(x,t)

 

[_Matt87_]

an infinitesimal change in the velocity of a free particle should yield an equivalent Lagrangian; that is, the difference must be of the form df(q,t)/dt. To first order, we have

L((v+\epsilon)^2) = L(v^2) + \frac{\partial L}{\partial v^2} 2 v \cdot \epsilon

For the two Lagrangians to be equivalent, the second term on the right must be linear in v, so L is proportional to v^2.

i don't understand one thing. please explain it.

if L(v'^2) must differ from L(v^2) only by the total time derivative, then \frac{\partial L}{\partial v^2} 2 v \cdot \epsilon should be equal to the right side of \frac{dL(v^2)}{dt}=\frac{\partial L(v^2)}{\partial v^2} \frac{dv^2}{dt} =\frac{\partial L(v^2)}{\partial v^2} 2v \frac{dv}{dt}

the question is. what does it mean that

the second term on the right must be linear in v, so L is proportional to v^2

??

 

[facenian]

the question is. what does it mean that ??

I guess it simply means that the total derivative of a function f(q,t) mus be linear in the derivates of q.

 

[_Matt87_]

ok. so the Lagrangian with infinitesimal change in the velocity is not equivalent to Lagrangian on the right side of the equation right? becouse the derivative is not linear to v but v^2. does it mean that Lagrangian with some infinitesimal change of velocity is just equal to lagrangian without it but plus something proportional to v^2 witch is just just the kinetic energy? what would happened if the derivative was the total derivative (linear to v)?

 

[facenian]

I think the problem with your reasoning is because you said a term like
\frac{dL(v^2)}{d t} takes place, this is not correct and it's not what sabastien said before. A term like the total time derivate of a function of v^2 does not yield a total derivate of coordenates and time only.