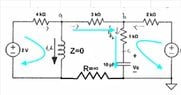
- #1
annamal
- 381
- 33
- Homework Statement
- Derive the governing equation for the voltage Vc across the capacitor
- Relevant Equations
- KCL and KVL
I was thinking about doing KVL around the circuit at the right but I noticed when the switch opens, the current through the circuit at the right is not the same throughout
-5 + Ic*2*1-^3 + Ic*10^3 = -Vc
Ic is not the same around the right circuit so I am stuck....
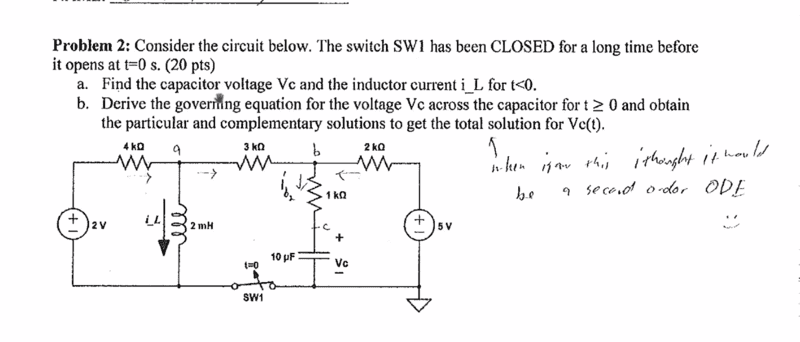
-5 + Ic*2*1-^3 + Ic*10^3 = -Vc
Ic is not the same around the right circuit so I am stuck....