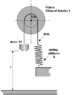
ok, i see a couple of problems with your approach. first, i am not sure where you get the formula \alpha=\omega^2 R. This is not true for SHM.
This leads to the second problem. you are attacking the problem as if were a statics problem, or as a constant acceleration problem. we need to start imagining this thing in motion. the mass is moving up and down and the spring is stretching and compressing. I would draw an x-axis beside the block and use that to measure where the block is at a giving time. let x=0 be the equilibrium position, this will be the most convenient. thus the motion is restricted to \pm A where A is the amplitude of the motion. this will help with visualization.
now, one major point of confusion is that we are going to have two \omega's which mean totally different things. first we have the angular speed of the wheel at any given time, call this \omega_w, and since the wheel will be changing speed all the time, this will be a function of time, so \omega_w=\omega_w(t).
the other will be the angular frequency of the SHM of the mass, let's just call that one \omega. this is the one that will be constant and is the answer to the problem, well \omega=2 \pi f and f is the answer.
so just to reiterate, \omega_w is the angular speed of the wheel, so \alpha_w=\frac{d \omega_w}{dt}=\frac{a}{R} where R is the radius of the wheel, and a is the linear acceleration of the mass. these are the quantities you want to use when applying Newton's second law to the wheel.
hopefully this will get you started in the right direction. this is a tricky problem, and i had to set up a differential equation (but not solve it) in order for \omega to make itself known.
good luck