toothpaste666
- 516
- 20
Hello everyone. I am attempting to teach myself about special relativity, and have learned a derivation for the Lorentz transformation. Before I go any farther I want to clear up the parts I don't understand right now and check that I am correct about the parts I do understand. Here I will derive the Lorentz transformation and ask a couple of questions as I go. I would greatly appreciate it if someone can help increase my understanding of these concepts.
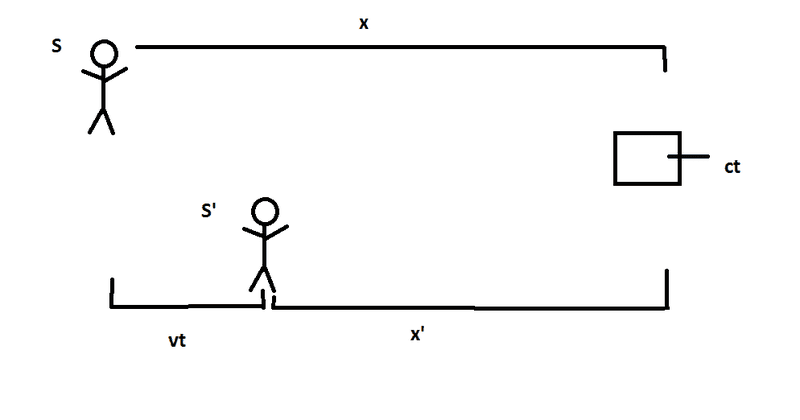
There will be two observers, S and S' that will start out with their x axis' lined up and the clocks they are carrying synched at t=0 and t'=0. S' will begin moving with speed v away from S who will remain stationary so that there is distance vt in between S and S'. S' will be moving toward a box that is moving at the speed of light c in the same direction as S'. I have made a picture of the situation. The distance between S and the box is x and the distance between S' and the box is x'. x=ct.
Here is my first question: From what I have learned it seems that not only does x=ct but x'=ct'. Is this only true because c is the same in every reference frame or would that also be true in Newtonian physics?
According to S': x = x' + vt'
According to S: x' = x - vt
plugging in x=ct into the second equation you have:
x' = ct-vt
x'=(c-v)t
Since distance is a velocity times a time and we know the time, that means the velocity that S' sees the box moving is less than c. But we know that c is the same in every reference frame. So our equations must be off by some factor.
Next question: From derivations I have seen on the internet, they add an error factor (lets call it 'f') into the two equations, so that they become this:
x = (x' + vt')f
x' = (x - vt)f
My question is: how do we know that we can use the same error factor for both equations? Wouldn't we use f for one and let's say g for the other? How can we prove that we can use the same for both? Forgive me if this is obvious, I am fairly new to these concepts.
Anyways we multiply the two equations together. (Is there a clear way to know whether to multiply, add or subtract two equations?) After multiplying them we get:
xx' = (x' +vt')(x-vt)f^2
xx' = (xx' - x'vt + xvt' - v^2tt')f^2
we know that x=ct and x'=ct' so t=x/c and t'=x'/c. plugging in we get:
xx' = (xx' - x'v(\frac{x}{c}) + xv(\frac{x'}{c}) - v^2(\frac{x}{c})(\frac{x'}{c}))f^2
xx' = (xx' - \frac{xx'v}{c} + \frac{xx'v}{c} - \frac{v^2xx'}{c^2}) f^2
xx' = (xx' - \frac{v^2xx'}{c^2})f^2
1 = (1 - \frac{v^2}{c^2})f^2
f^2 = \frac{1}{1-\frac{v^2}{c^2}}
f = \sqrt{\frac{1}{1-\frac{v^2}{c^2}}}
f = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}
which is the lorentz transformation. Any feedback would be greatly appreciated. :)
There will be two observers, S and S' that will start out with their x axis' lined up and the clocks they are carrying synched at t=0 and t'=0. S' will begin moving with speed v away from S who will remain stationary so that there is distance vt in between S and S'. S' will be moving toward a box that is moving at the speed of light c in the same direction as S'. I have made a picture of the situation. The distance between S and the box is x and the distance between S' and the box is x'. x=ct.
Here is my first question: From what I have learned it seems that not only does x=ct but x'=ct'. Is this only true because c is the same in every reference frame or would that also be true in Newtonian physics?
According to S': x = x' + vt'
According to S: x' = x - vt
plugging in x=ct into the second equation you have:
x' = ct-vt
x'=(c-v)t
Since distance is a velocity times a time and we know the time, that means the velocity that S' sees the box moving is less than c. But we know that c is the same in every reference frame. So our equations must be off by some factor.
Next question: From derivations I have seen on the internet, they add an error factor (lets call it 'f') into the two equations, so that they become this:
x = (x' + vt')f
x' = (x - vt)f
My question is: how do we know that we can use the same error factor for both equations? Wouldn't we use f for one and let's say g for the other? How can we prove that we can use the same for both? Forgive me if this is obvious, I am fairly new to these concepts.
Anyways we multiply the two equations together. (Is there a clear way to know whether to multiply, add or subtract two equations?) After multiplying them we get:
xx' = (x' +vt')(x-vt)f^2
xx' = (xx' - x'vt + xvt' - v^2tt')f^2
we know that x=ct and x'=ct' so t=x/c and t'=x'/c. plugging in we get:
xx' = (xx' - x'v(\frac{x}{c}) + xv(\frac{x'}{c}) - v^2(\frac{x}{c})(\frac{x'}{c}))f^2
xx' = (xx' - \frac{xx'v}{c} + \frac{xx'v}{c} - \frac{v^2xx'}{c^2}) f^2
xx' = (xx' - \frac{v^2xx'}{c^2})f^2
1 = (1 - \frac{v^2}{c^2})f^2
f^2 = \frac{1}{1-\frac{v^2}{c^2}}
f = \sqrt{\frac{1}{1-\frac{v^2}{c^2}}}
f = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}
which is the lorentz transformation. Any feedback would be greatly appreciated. :)
Attachments
Last edited: